---

Big Theta(Θ)

---

This notation is denoted by ‘Θ’, and it is pronounced as “Big Theta”. Big Theta notation defines tight bound for the algorithm. It means the running time of algorithm is between upper bound and lower bound

Definition

The function f(n)=Θ(g(n)) iff there exist positive constants c1,c2 and n0 such that c1*g(n) ≤ f(n) ≤ c2*g(n) for all n, n ≥ n0. 

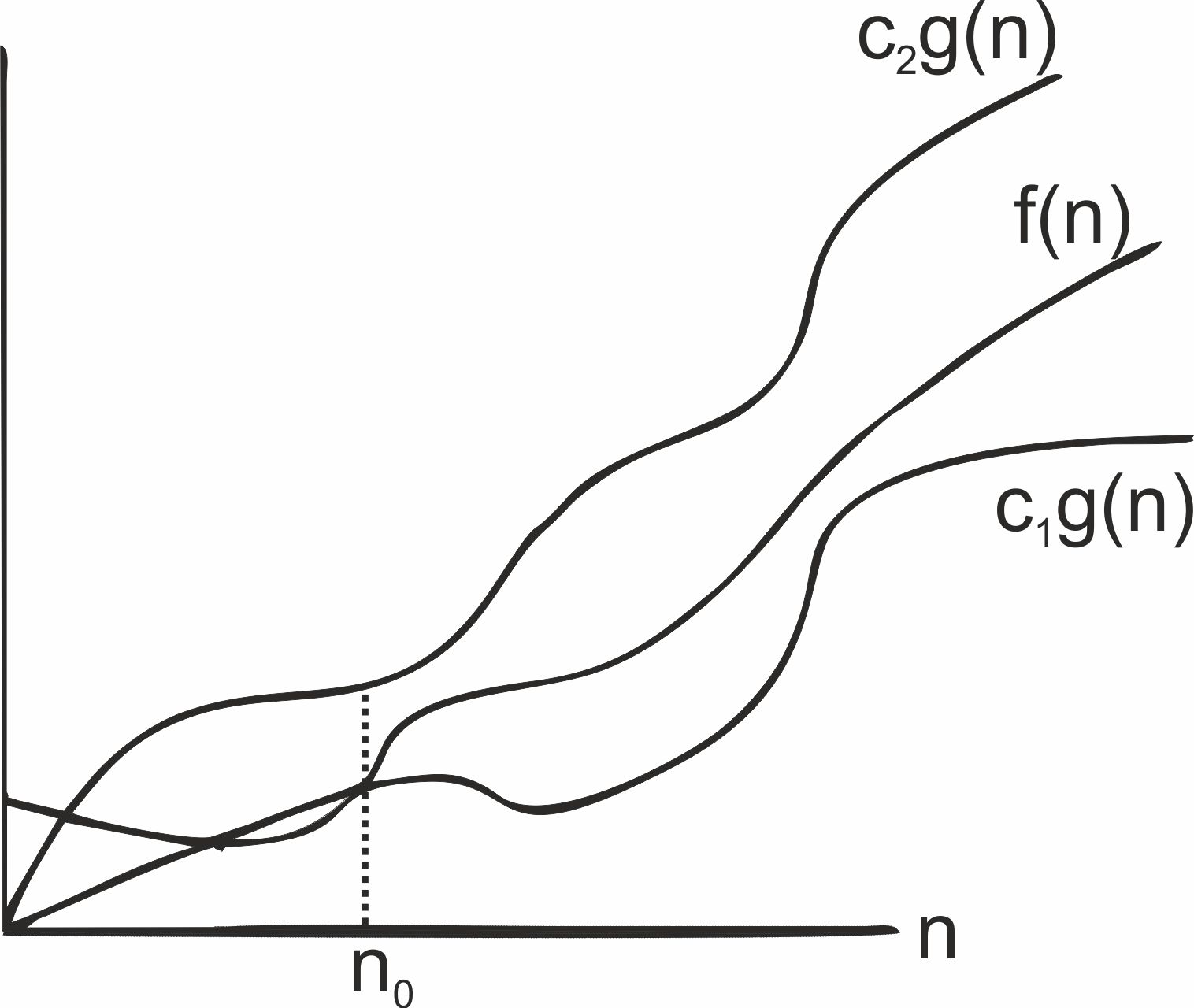
The theta notation is more precise that both the big oh and omega notations. The function f(n) = Θ(g(n)) iff g(n) is both an upper and lower bound of f(n).

Examples:

1. 3n+2 = Θ(n)
    as 3n+2≥3n and 3n+2≤ 4n, for n ≥ 2.
    c₁=3, c₂=4, and n₀=2

---

Next Topic :Introduction