Machine Learning - (LAB PROGRAMS)

Week 4

☛ Write a Python program to implement Simple Linear Regression.

Solution :

Linear regression is a statistical method used to model the relationship between a dependent variable and one or more independent variables. It provides valuable insights for prediction and data analysis. This article will explore its types, assumptions, implementation, advantages, and evaluation metrics.

Simple Linear Regression:

Simple linear regression is the simplest form of linear regression and it involves only one independent variable and one dependent variable.

The equation for simple linear regression is:

	y = β0 + β1 X 

		where:
			y is the dependent variable
			X is the independent variable
			β0 is the intercept
			β1 is the slope

Step-1: Data Pre-processing

The first step for creating the Simple Linear Regression model is data pre-processing

Step-2: Fitting the Simple Linear Regression to the Training Set:

Now the second step is to fit our model to the training dataset. To do so, we will import the LinearRegression class of the linear_model library from the scikit learn.

Step: 3. Prediction of test set result:

dependent (salary) and an independent variable (Experience). So, now, our model is ready to predict the output for the new observations. In this step, we will provide the test dataset (new observations) to the model to check whether it can predict the correct output or not.

Step: 4. visualizing the results:

Now in this step, we will visualize the training set result. To do so, we will use the scatter() function of the pyplot library, which we have already imported in the pre-processing step. The scatter () function will create a scatter plot of observations.

Library Installation:

To install required library files, Open Command Prompt or Terminal and execute the following commands


$ pip install scikit-learn

$ pip install pandas

$ pip install matplotlib

CSV file : "salary_data.csv"


age,salary
22,30000
25,35000
30,45000
35,50000
40,60000
45,65000
50,70000
55,80000

To Download above CSV file : Click Here

Source Code:

File Name: Linear_Regression.py


import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_absolute_error,mean_squared_error,r2_score

#Load the data from the CSV file
data = pd.read_csv('salary_data.csv')
x= data[['age']] # Independent variable
y = data['salary'] # Dependent variable

#Split the data into training and testing sets
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2,random_state=1)

model=LinearRegression()
model.fit(x_train, y_train)

y_pred=model.predict(x_test)

#Model coefficients
print(f"Intercept (a0): {model.intercept_}")
print(f"Slope (a1): {model.coef_}")
r2=r2_score(y_test, y_pred)

#Print evaluation metrics
print (f"R-squared Score: ",r2)

#User input for age
user_age = float(input("Enter age to predict salary: "))

#Predict salary for the given age
predicted_salary = model.predict(pd.DataFrame([[user_age]], columns=['age']))
print (f"The predicted salary for age {user_age} is:",predicted_salary)
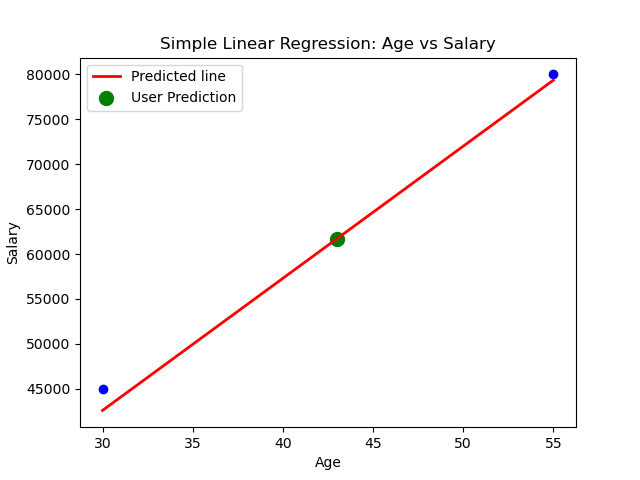
plt.scatter (x_test, y_test, color='blue')
plt.plot(x_test, y_pred, color='red', linewidth=2, label='Predicted line')
plt.scatter (user_age, predicted_salary, color='green', s=100, label='User Prediction')
plt.xlabel('Age')
plt.ylabel('Salary')
plt.title('Simple Linear Regression: Age vs Salary')
plt.legend()
plt.show()

Output:


Sample Run:
--------------
$ python3 Linear_Regression.py
Intercept (a0): -1522.5102319235884
Slope (a1): [1470.66848568]
R-squared Score:  0.9899167950543547
Enter age to predict salary: 43
The predicted salary for age 43.0 is: [61716.23465211]

Machine Learning Lab Programs

1) Write a python program to compute
• Central Tendency Measures: Mean, Median,Mode
• Measure of Dispersion: Variance, Standard Deviation View Solution

2) Study of Python Basic Libraries such as Statistics, Math, Numpy and Scipy View Solution

3) Study of Python Libraries for ML application such as Pandas and Matplotlib View Solution

4) Write a Python program to implement Simple Linear Regression View Solution

5) Implementation of Multiple Linear Regression for House Price Prediction using sklearn View Solution

6) Implementation of Decision tree using sklearn and its parameter tuning View Solution

7) Implementation of KNN using sklearn View Solution

8) Implementation of Logistic Regression using sklearn View Solution

9) Implementation of K-Means Clustering View Solution

10) Performance analysis of Classification Algorithms on a specific dataset (Mini Project) View Solution

Menu