---

Architecture Design

---

The word architecture refers to the overall structure of the network: how many units it should have and how these units should be connected to each other.

Generic Neural Architectures

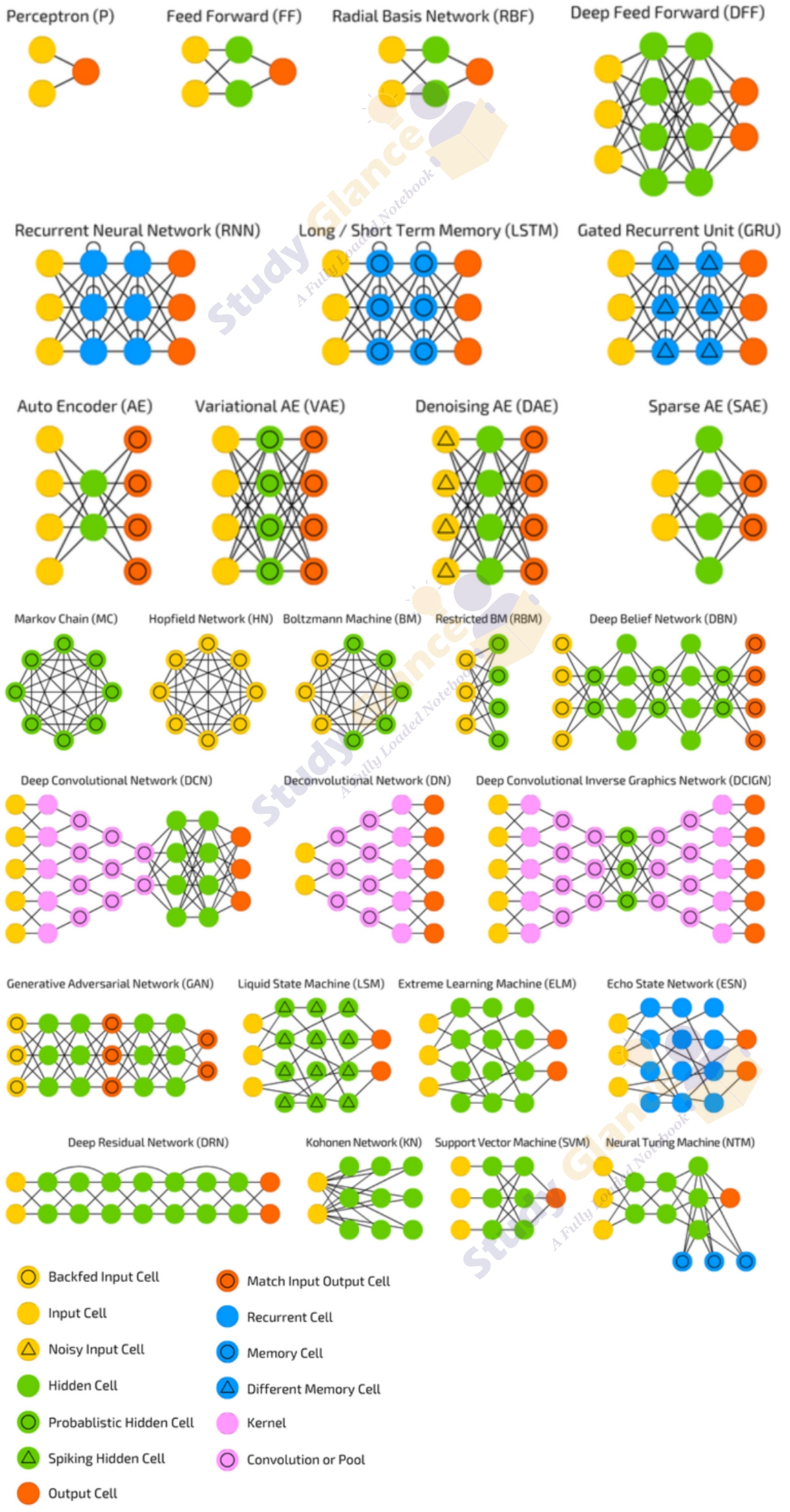
Most neural networks are organized into groups of units called layers. Most neural network architectures arrange these layers in a chain structure, with each layer being a function of the layer that preceded it. In this structure, the first layer is given by

$h^{\left(1\right)}=g^{\left(1\right)}(W^{\left(1\right)\mathrm{T}}x+b^{\left(1\right)})$

the second layer is given by

$h^{\left(2\right)}=g^{\left(2\right)}(W^{\left(2\right)\mathrm{T}}{h}^{\left(1\right)}+b^{\left(2\right)})$

In these chain-based architectures, the main architectural considerations are to choose the depth of the network and the width of each layer.

Universal Approximation Properties and Depth

A feed-forward network with a single hidden layer containing a finite number of neurons can approximate continuous functions on compact subsets of ℝⁿ, under mild assumptions on the activation function

• Simple neural networks can represent a wide variety of interesting functions when given appropriate parameters
• However, it does not touch upon the algorithmic learnability of those parameters

The universal approximation theorem means that regardless of what function we are trying to learn, we know that a large MLP will be able to represent this function. However, we are not guaranteed that the training algorithm will be able to learn that function. Even if the MLP is able to represent the function, learning can fail for two different reasons.

1. Optimizing algorithms may not be able to find the value of the parameters that corresponds to the desired function.
2. The training algorithm might choose wrong function due to over-fitting

The universal approximation theorem says that there exists a network large enough to achieve any degree of accuracy we desire, but the theorem does not say how large this network will be. provides some bounds on the size of a single-layer network needed to approximate a broad class of functions. Unfortunately, in the worse case, an exponential number of hidden units may be required. This is easiest to see in the binary case: the number of possible binary functions on vectors $v\in {\left\{\mathrm{0,1}\right\}}^{\mathrm{n}}$ is $2^{2^{\mathrm{n}}}$ and selecting one such function requires $2^{\mathrm{n}}$ bits, which will in general require $O\left(2^{\mathrm{n}}\right)$ degrees of freedom.

A feedforward network with a single layer is sufficient to represent any function, But the layer may be infeasibly large and may fail to generalize correctly. Using deeper models can reduce no.of units required and reduce generalization error

---

Next Topic :Dataset Augmentation