---

Adaptive Linear Neuron

---

Adaptive Linear Neuron (Adaline)

Adaline which stands for Adaptive Linear Neuron, is a network having a single linear unit. It was developed by Widrow and Hoff in 1960. Some important points about Adaline are as follows −

• It uses bipolar activation function.
• Adaline neuron can be trained using Delta rule or Least Mean Square(LMS) rule or widrow-hoff rule
• The net input is compared with the target value to compute the error signal.
• on the basis of adaptive training algoritham weights are adjusted

The basic structure of Adaline is similar to perceptron having an extra feedback loop with the help of which the actual output is compared with the desired/target output. After comparison on the basis of training algorithm, the weights and bias will be updated.

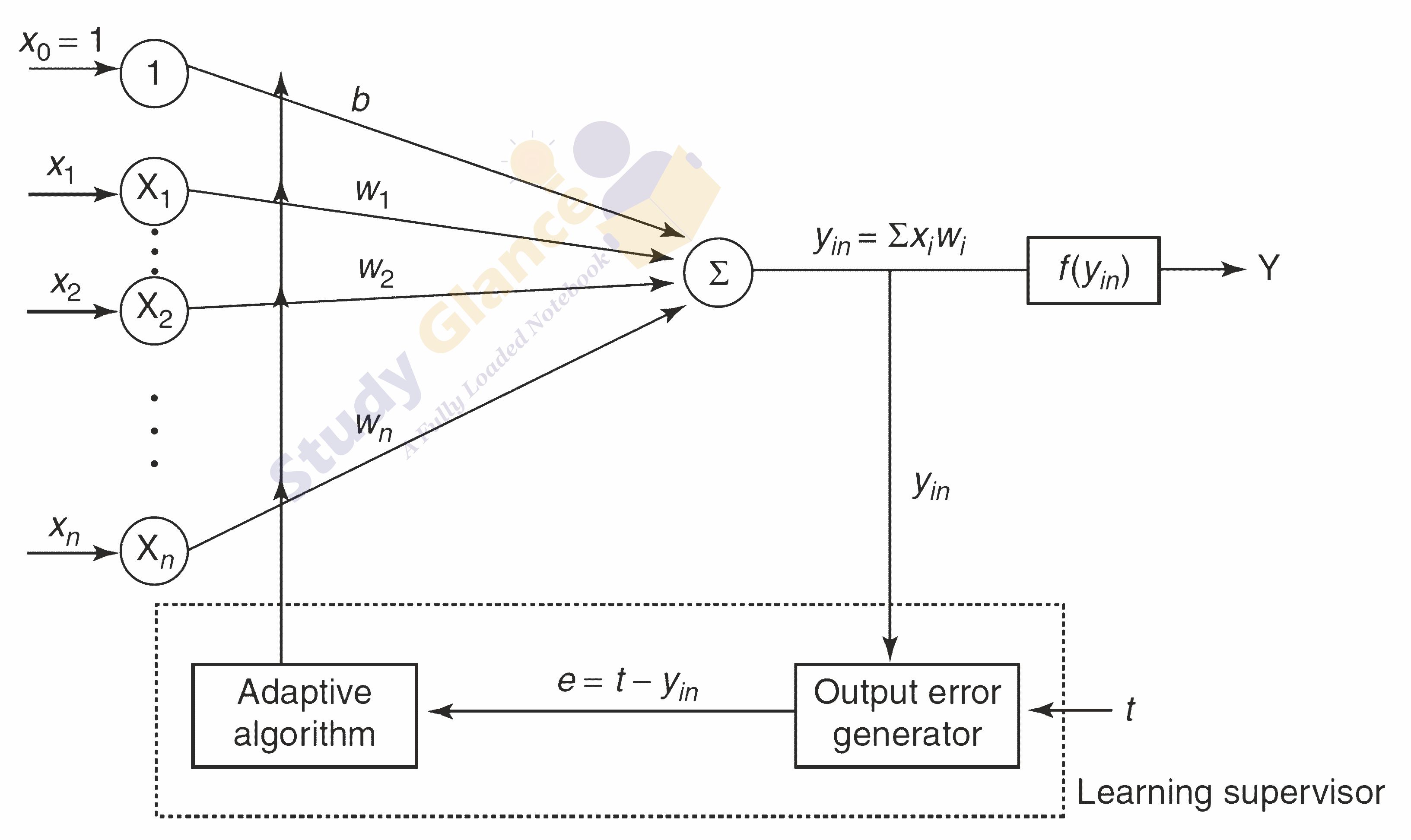
Adaptive Linear Neuron Learning algorithm

Step 0: initialize the weights and the bias are set to some random values but not to zero, also initialize the learning rate α.

Step 1 − perform steps 2-7 when stopping condition is false.

Step 2 − perform steps 3-5 for each bipolar training pair s:t.

Step 3 − Activate each input unit as follows −

$$x_i=s_i(i=1ton)$$

Step 4 − Obtain the net input with the following relation −

$$y_{in}=\underset{i}{\overset{n}{\sum <!--\; \sum \; -->}}{x}_i.w_i+\mathrm{b}$$

Here ‘b’ is bias and ‘n’ is the total number of input neurons.

Step 5 Until least mean square is obtained (t - y_in), Adjust the weight and bias as follows −

      w_i(new) = w_i(old) + α(t - y_in)x_i
      b(new) = b(old) + α(t - y_in)

Now calculate the error using => E = (t - y_in)²

Step 7 − Test for the stopping condition, if error generated is less then or equal to specified tolerance then stop.

---

---

Multiple Adaptive Linear Neuron (Madaline)

Madaline which stands for Multiple Adaptive Linear Neuron, is a network which consists of many Adalines in parallel. It will have a single output unit. Some important points about Madaline are as follows −

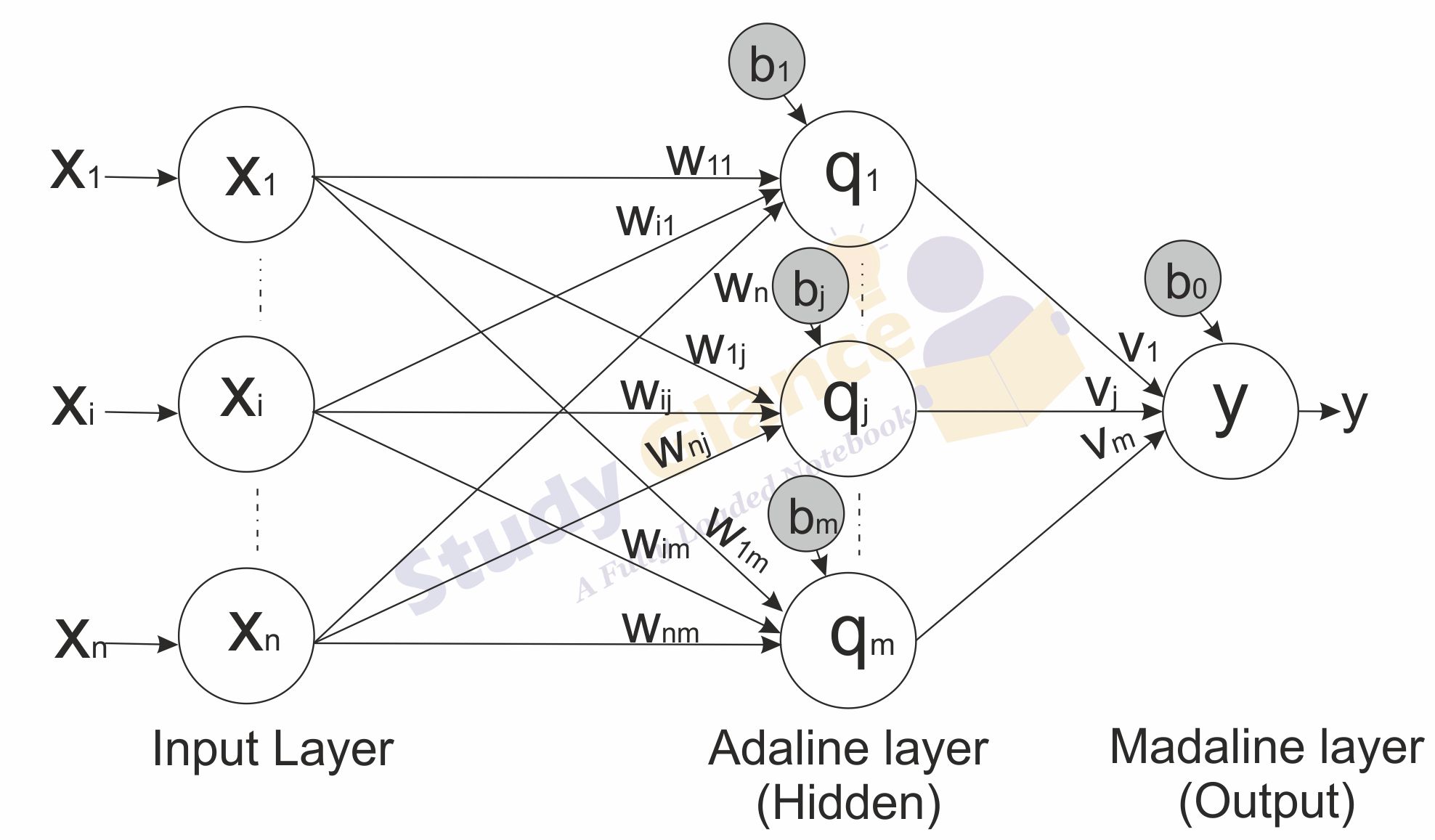
• It is just like a multilayer perceptron, where Adaline will act as a hidden unit between the input and the Madaline layer.
• The weights and the bias between the input and Adaline layers, as in we see in the Adaline architecture, are adjustable.
• The Adaline and Madaline layers have fixed weights and bias of 1.
• Training can be done with the help of Delta rule.

It consists of “n” units of input layer and “m” units of Adaline layer and “1” unit of the Madaline layer. Each neuron in the Adaline and Madaline layers has a bias of excitation “1”. The Adaline layer is present between the input layer and the Madaline layer; the Adaline layer is considered as the hidden layer.

Multiple Adaptive Linear Neuron (Madaline) Training Algorithm

By now we know that only the weights and bias between the input and the Adaline layer are to be adjusted, and the weights and bias between the Adaline and the Madaline layer are fixed.

Step 0 − initialize the weights and the bias(for easy calculation they can be set to zero). also initialize the learning rate α(0, α, 1) for simpicity α is set to 1.

Step 1 − perform steps 2-6 when stopping condition is false.

Step 2 − perform steps 3-5 for each bipolar training pair s:t

Step 3 − Activate each input unit as follows −

$$x_i=s_i(i=1ton)$$

Step 4 − Obtain the net input at each hidden layer, i.e. the Adaline layer with the following relation −

$$Q_{inj}=b_j+{\displaystyle \underset{i}{\overset{n}{\sum <!--\; \sum \; -->}}{x}_i{w}_{ij}(j=1tom)}$$

Here ‘b’ is bias and ‘n’ is the total number of input neurons.

Step 5 − Apply the following activation function to obtain the final output at the Adaline and the Madaline layer −

$$f(x)=\{\begin{array}{ll}1& ifx⩾<!--\; ⩾\; -->0\\ -<!--\; -\; -->1& ifx<0\end{array}$$

Output at the hidden (Adaline) unit

$$Q_j=f(Q_{inj})$$

Final output of the network

i.e. $y_{inj}=b_0+\underset{j=1}{\overset{m}{\sum <!--\; \sum \; -->}}{Q}_j{v}_j$

$$y=f(y_{in})$$

Step 6 − Calculate the error and adjust the weights as follows −

If t ≠ y and t = +1, update weights on Z_j, where net input is closest to 0 (zero)
      w_ij(new) = w_ij(old) + α(1 - Q_inj)x_i
      b_j(new) = b_j(old) + α(1 - Q_inj)

else If t ≠ y and t = -1, update weights on Z_k, whose net input is positive
      w_ik(new) = w_ik(old) + α(-1 - Q_ink)x_i
      b_k(new) = b_k(old) + α(-1 - Q_ink)

else if y = t then
      no weight updation is required.

Step 7 − Test for the stopping condition, which will happen when there is no change in weight or the highest weight change occurred during training is smaller than the specified tolerance.

---

Next Topic :Back Propagation