NN Menu

Bidirectional Associative Memory

Bidirectional Associative Memory (BAM)

Bidirectional associative memory (BAM), first proposed by Bart Kosko in the year 1988. The BAM network performs forward and backward associative searches for stored stimulus responses. The BAM is a recurrent hetero associative pattern-marching nerwork that encodes binary or bipolar patterns using Hebbian learning rule. It associates patterns, say from set A to patterns from set B and vice versa is also performed. BAM neural nets can respond to input from either layers (input layer and output layer).

Bidirectional Associative Memory Architecture

The architecture of BAM network consists of two layers of neurons which are connected by directed weighted pare interconnecrions. The network dynamics involve two layers of interaction. The BAM network iterates by sending the signals back and forth between the two layers until all the neurons reach equilibrium. The weights associated with the network are bidirectional. Thus, BAM can respond to the inputs in either layer.

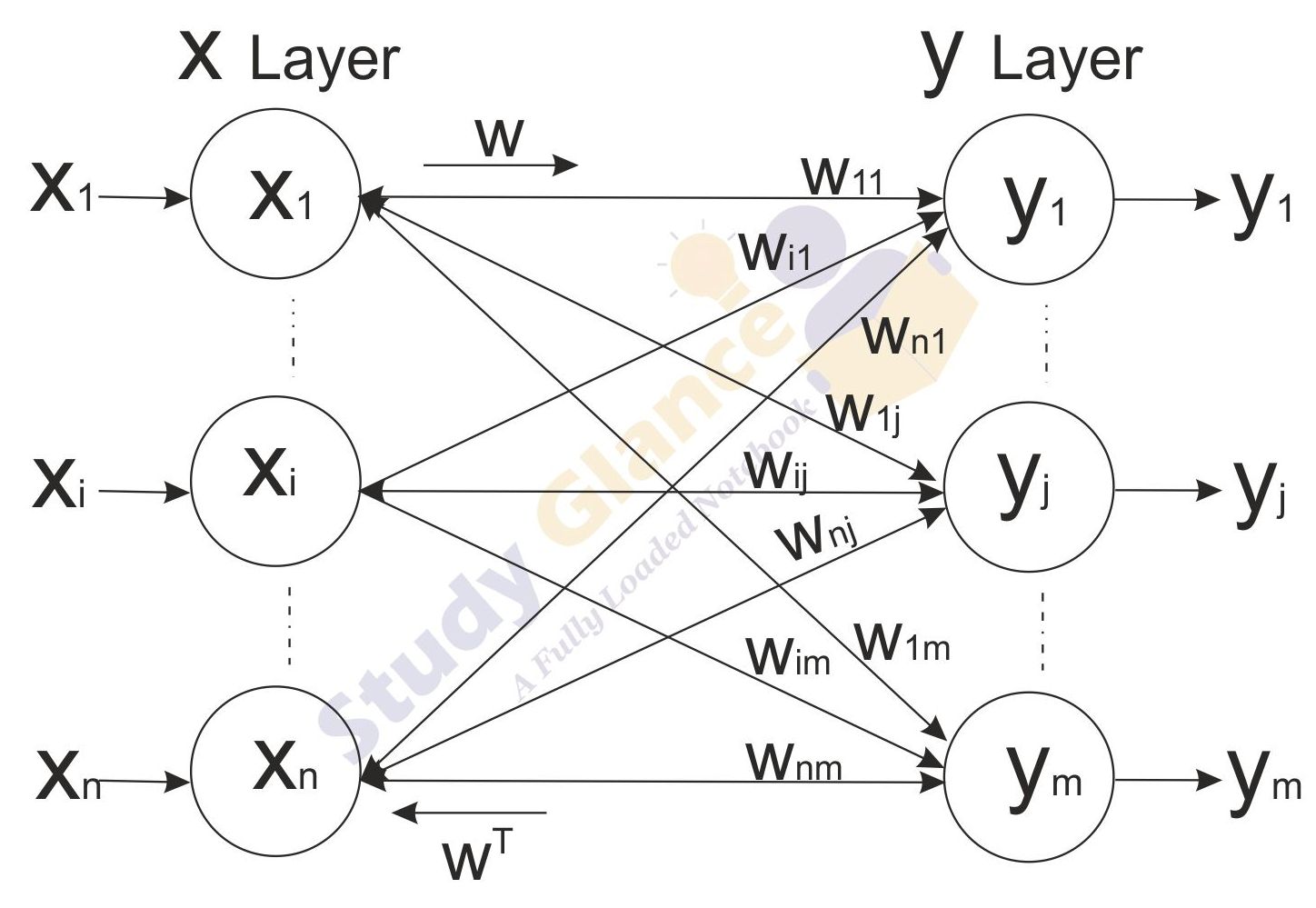
Figure shows a BAM network consisting of n units in X layer and m units in Y layer. The layers can be connected in both directions(bidirectional) with the result the weight matrix sent from the X layer to the Y layer is W and the weight matrix for signals sent from the Y layer to the X layer is W^T. Thus, the Weight matrix is calculated in both directions.

Determination of Weights

Let the input vectors be denoted by s(p) and target vectors by t(p). p = 1, ... , P. Then the weight matrix to store a set of input and target vectors, where

s(p) = (s₁(p), .. , s_i(p), ... , s_n(p))
t(p) = (t₁(p), .. , t_j(p), ... , t_m(p))

can be determined by Hebb rule training a1gorithm. In case of input vectors being binary, the weight matrix W = {w_ij} is given by

$w_{i j} = \sum_{p = 1}^{P} [2 s_{i} (p) - 1] [2 t_{j} (p) - 1]$

When the input vectors are bipolar, the weight matrix W = {w_ij} can be defined as

$w_{i j} = \sum_{p = 1}^{P} [s_{i} (p)] [t_{j} (p)]$

The activation function is based on whether the input target vector pairs used are binary or bipolar

The activation function for the Y-layer

1. With binary input vectors is

y_{j} = {\begin{cases} 1 & i f y_{i n j} > 0 \\ y_{j} & i f y_{i n j} = 0 \\ 0 & i f y_{i n j} < 0 \end{cases}

2. With bipolar input vectors is

y_{j} = {\begin{cases} 1 & i f y_{i n j} > θ_{i} \\ y_{j} & i f y_{i n j} = θ_{j} \\ -1 & i f y_{i n j} < θ_{j} \end{cases}

The activation function for the X-layer

1. With binary input vectors is

x_{i} = {\begin{cases} 1 & i f x_{i n i} > 0 \\ x_{i} & i f x_{i n i} = 0 \\ 0 & i f x_{i n i} < 0 \end{cases}

2. With bipolar input vectors is

x_{i} = {\begin{cases} 1 & i f x_{i n i} > θ_{i} \\ x_{i} & i f x_{i n i} = θ_{i} \\ -1 & i f x_{i n i} < θ_{i} \end{cases}

Testing Algorithm for Discrete Bidirectional Associative Memory

Step 0: Initialize the weights to srore p vectors. Also initialize all the activations to zero. Step 1: Perform Steps 2-6 for each testing input. Step 2: Ser the activations of X layer to current input pauern, i.e., presenting the input pattern x to X layer and similarly presenting the input pattern y to Y layer. Even though, it is bidirectional memory, at one time step, signals can be sent from only one layer. So, either of the input patterns may be the zero vector Step 3: Perform Steps 4-6 when the acrivacions are not converged. Step 4: Update the activations of units in Y layer. Calculate the net input,

y_{i n j} = \sum_{i = 1}^{n} x_{i} w_{i j}

Applying ilie activations, we obtain

y_{j} = f (y_{i n j})

Send this signal to the X layer.

Step 5: Updare the activations of unirs in X layer. Calculate the net input,

x_{i n i} = \sum_{j = 1}^{m} y_{j} w_{i j}

Applying ilie activations, we obtain

x_{i} = f (x_{i n i})

Send this signal to the Y layer.

Step 6: Test for convergence of the net. The convergence occurs if the activation vectors x and y reach equilibrium. If this occurs then stop, Otherwise, continue.

Next Topic :Hopfield Networks