---

Associate Memory Network

---

Associative Memory Networks

An associative memory network can store a set of patterns as memories. When the associative memory is being presented with a key pattern, it responds by producing one of the stored patterns, which closely resembles or relates to the key panern. Thus, the recall is through association of the key pattern, with the help of informtion memorized. These types of memories are also called as content-addressable memories (CAM). The CAM can also be viewed as associating data to address, i.e.; for every data in the memory there is a corresponding unique address. Also, it can be viewed as data correlator. Here inpur data is correlated with that of the stored data in the CAM. It should be nored that the stored patterns must be unique, i.e., different patterns in each location. If the same pattern exists in more than one locacion in the CAM, then, even though the correlation is correct, the address is noted to be ambiguous. Associative memory makes a parallel search within a stored data file. The concept behind this search is to Output any one or all stored items Which match the given search argumemt.

---

---

Training Algorithms for Pattern Association

There are two algorithms developed for training of pattern association nets.

1. Hebb Rule
2. Outer Products Rule

1. Hebb Rule

The Hebb rule is widely used for finding the weights of an associative memory neural network. The training vector pairs here are denoted as s:t. The weights are updated unril there is no weight change.

Hebb Rule Algorithmic

Step 0: Set all the initial weights to zero, i.e.,
W_ij = 0    (i = 1 to n, j = 1 to m)

Step 1: For each training target input output vector pairs s:t, perform Steps 2-4.

Step 2: Activate the input layer units to current training input, X_i=S_i (for i = 1 to n)

Step 3: Activate the output layer units to current target output,
y_j = t_j (for j = 1 to m)

Step 4: Start the weight adjustment
$$w_{ij}(new)=w_{ij}(old)+x_i{y}_j(i=1tonj=1tom)$$

2. Outer Products Rule

Outer products rule is a method for finding weights of an associative net.

Input=> s = (s₁, ... ,s_i, ... ,s_n)
Output=> t= (t₁, ... ,t_j, ... ,t_m)

The outer product of the two vectors is the product of the matrices S = s^T and T = t, i.e., between [n X 1] marrix and [1 x m] matrix. The transpose is to be taken for the input matrix given.

ST = s^Tt      =>

$\left[\begin{array}{c}{s}_1\\ \mathrm{.}\\ \mathrm{.}\\ s_{\mathrm{i}}\\ \mathrm{.}\\ \mathrm{.}\\ s_{\mathrm{n}}\end{array}\right]*\left[\begin{array}{ccccccc}{t}_1& \mathrm{.}& \mathrm{.}& t_{\mathrm{j}}& \mathrm{.}& \mathrm{.}& t_{\mathrm{m}}\end{array}\right]$

This weight matrix is same as the weight matrix obtained by Hebb rule to store the pattern association s:t. For storing a set of associations, s(p):t(p), p = 1 to P, wherein,
s(p) = (s₁ (p}, ... , s_i(p), ... , s_n(p))
t(p) = (t₁ (p), · · ·' t_j(p), · · · 't_m(p))

the weight matrix W = {w_ij} can be given as

$$\mathrm{w}={\displaystyle \sum _{p=1}^n{S}^{\mathrm{T}}(p).\mathrm{S}(p)}$$

---

---

There two types of associative memories

• Auto Associative Memory
• Hetero Associative memory

Auto Associative Memory

An auto-associative memory recovers a previously stored pattern that most closely relates to the current pattern. It is also known as an auto-associative correlator.

In the auto associative memory network, the training input vector and training output vector are the same

Auto Associative Memory Algorithm

Training Algorithm

For training, this network is using the Hebb or Delta learning rule.

Step 1 − Initialize all the weights to zero as w_ij = 0 i=1ton, j=1ton

Step 2 − Perform steps 3-4 for each input vector.

Step 3 − Activate each input unit as follows − $$x_i=s_i(i=1ton)$$

Step 4 − Activate each output unit as follows − $$y_j=s_j(j=1ton)$$

Step 5 − Adjust the weights as follows − $$w_{ij}(new)=w_{ij}(old)+x_i{y}_j$$

The weight can also be determine form the Hebb Rule or Outer Products Rule learning $$\mathrm{w}={\displaystyle \underset{p=1}{\overset{n}{\sum <!--\; \sum \; -->}}{S}^{\mathrm{T}}(p).\mathrm{S}(p)}$$

Testing Algorithm

Step 1 − Set the weights obtained during training for Hebb’s rule.

Step 2 − Perform steps 3-5 for each input vector.

Step 3 − Set the activation of the input units equal to that of the input vector.

Step 4 − Calculate the net input to each output unit j = 1 to n; $$y_{inj}={\displaystyle \underset{i=1}{\overset{n}{\sum <!--\; \sum \; -->}}{x}_i{w}_{ij}}$$

Step 5 − Apply the following activation function to calculate the output $$y_j=f(y_{inj})=\{\begin{array}{ll}+1& if{y}_{inj}>0\\ -<!--\; -\; -->1& if{y}_{inj}⩽<!--\; ⩽\; -->0\end{array}$$

Hetero Associative memory

In a hetero-associate memory, the training input and the target output vectors are different. The weights are determined in a way that the network can store a set of pattern associations. The association here is a pair of training input target output vector pairs (s(p), t(p)), with p = 1,2,…p. Each vector s(p) has n components and each vector t(p) has m components. The determination of weights is done either by using Hebb rule or delta rule. The net finds an appropriate output vector, which corresponds to an input vector x, that may be either one of the stored patterns or a new pattern.

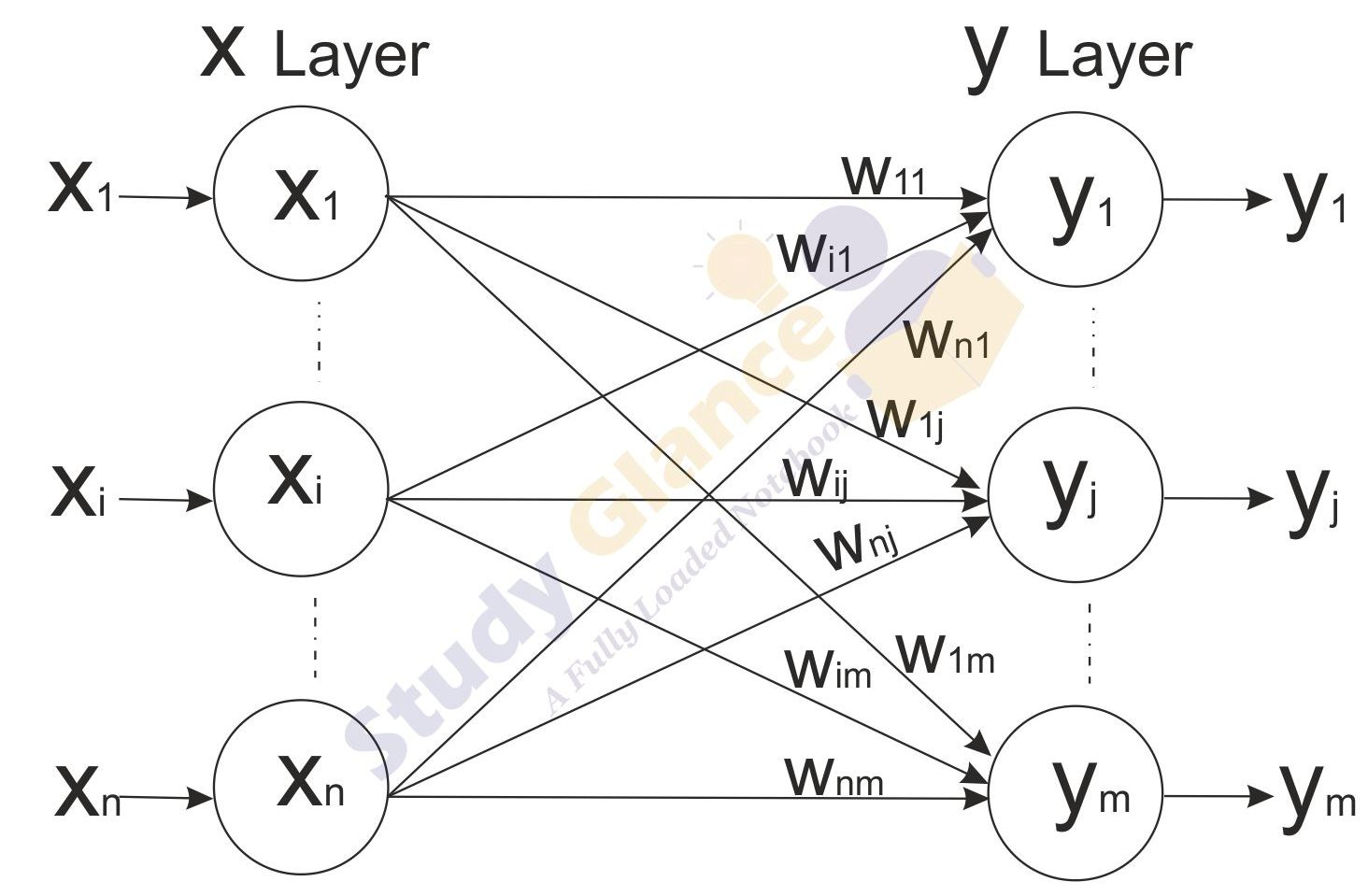
Hetero Associative Memory Algorithm

Training Algorithm

Step 1 − Initialize all the weights to zero as w_ij = 0 i= 1 to n, j= 1 to m

Step 2 − Perform steps 3-4 for each input vector.

Step 3 − Activate each input unit as follows − $$x_i=s_i(i=1ton)$$

Step 4 − Activate each output unit as follows − $$y_j=s_j(j=1tom)$$

Step 5 − Adjust the weights as follows − $$w_{ij}(new)=w_{ij}(old)+x_i{y}_j$$

The weight can also be determine form the Hebb Rule or Outer Products Rule learning $$\mathrm{w}={\displaystyle \underset{p=1}{\overset{n}{\sum <!--\; \sum \; -->}}{S}^{\mathrm{T}}(p).\mathrm{S}(p)}$$

Testing Algorithm

Step 1 − Set the weights obtained during training for Hebb’s rule.

Step 2 − Perform steps 3-5 for each input vector.

Step 3 − Set the activation of the input units equal to that of the input vector.

Step 4 − Calculate the net input to each output unit j = 1 to m; $$y_{inj}={\displaystyle \underset{i=1}{\overset{n}{\sum <!--\; \sum \; -->}}{x}_i{w}_{ij}}$$

Step 5 − Apply the following activation function to calculate the output $$y_j=f(y_{inj})=\{\begin{array}{ll}+1& if{y}_{inj}>0\\ 0& if{y}_{inj}=0\\ -<!--\; -\; -->1& if{y}_{inj}<0\end{array}$$

---

Next Topic :Bidirectional Associative Memory