Red Black Tree
Red black tree is a binary search tree in which every node is colored either red or black. Each node in a Red-Black Tree has an extra bit for denoting the color of the node, either red or black.
Properties of Red Black Tree
- Every node is either red or black.
- The root is always black.
- All leaves (NIL nodes) are black.
- Red nodes can't have red children (no two red nodes can be adjacent).
- Every path from a node to its descendant NIL nodes has the same number of black nodes.
1. Insertion Operations of Red Black Tree
Insertion in a Red-Black Tree starts like a regular binary search tree insertion and then makes adjustments to maintain the Red-Black properties.
Steps for Insertion:
- Insert the Node: Insert the new node like in a binary search tree. New nodes are always inserted as red nodes.
- ROOT Node: If new node is root, change color of new node as BLACK.
- Check for Violations: After insertion, check for Red-Black Tree property violations and fix them using Recoloring or Rotations followed by Recoloring.
- Recoloring: If a parent and uncle are red then
a) Change color of parent and uncle as BLACK.
b) color of grand parent as RED if not ROOT.
c) repeat steps a and b till we reach the ROOT. - Rotations followed by Recoloring: If the parent is red but the uncle is black then, perform rotations. There are four cases:
a) Left-Left (LL) Case and swap the colors of grand parent and parent.
b) Left-Right (LR) Case and swap the colors of grand parent and new node.
c) Right-Right (RR) Case and swap the colors of grand parent and parent.
d) Right-Left (RL) Case and swap the colors of grand parent and new node.
- Recoloring: If a parent and uncle are red then
Algorithm for Insertion Operations ofRed Black Tree
RB-INSERT(T, k)
BST-INSERT(T, k) //normal BST insertion
while k.parent.color == RED
if k.parent == k.parent.parent.right
u = k.parent.parent.left //uncle
if u.color == RED
u.color = BLACK
k.parent.color = BLACK
k.parent.parent.color = RED
k = k.parent.parent
else if k == k.parent.left
k = k.parent
LEFT-ROTATE(T, k)
k.parent.color = BLACK
k.parent.parent.color = RED
RIGHT-ROTATE(T, k.parent.parent)
else (same as then clause with “left” and “right” exchanged)
T.root.color = BLACKExample: Construct an Red Black Tree by inserting numbers 1,2,3,4,5,6,7,8.
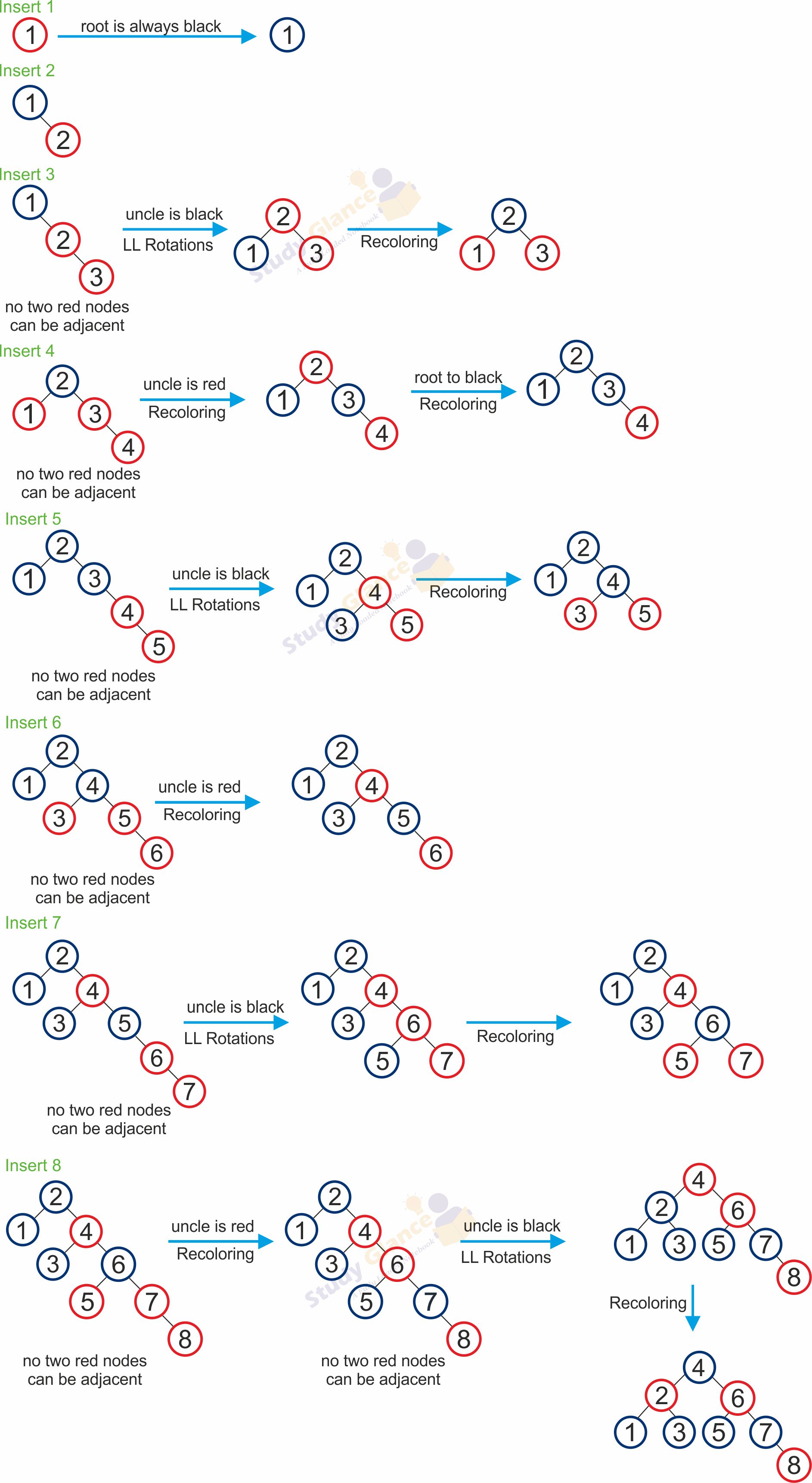
2. Deletion Operations of Red Black Tree
Deletion operations in a Red-Black Tree (RBT) can be quite complex due to the balancing rules that need to be maintained. In delete operation, we check color of sibling to decide the appropriate case. In delete, the main violated property is, in each path the same number of black nodes.
Steps for Deletion:
1. Find the Node: Like in a regular binary search tree, find the node that needs to be deleted.
2. Perform Standard BST Delete:
- Case 1:
- If node to be deleted is red (leaf node), then delete it.
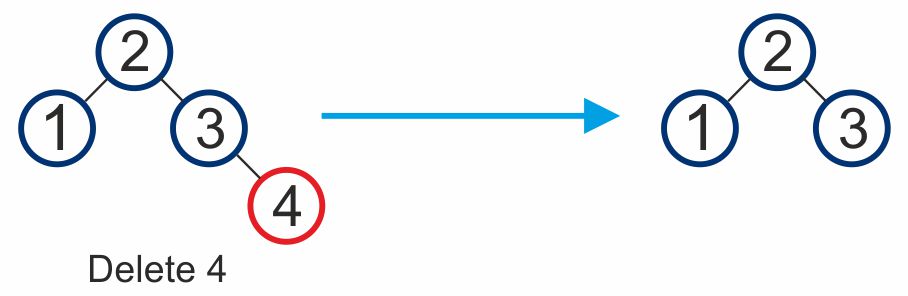
- If node to be deleted is black (leaf node) replace with null & DB(Double Black)
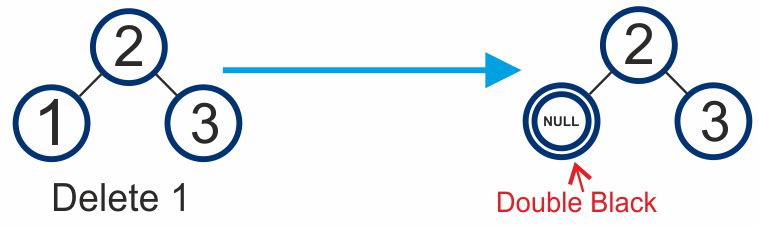
- If node to be deleted is red (leaf node), then delete it.
- Case-2: if root is DB, just remove DB

- Case-3: if DB sibling is black & its both children's are black
- Remove DB
- Change the color of sibling to red
- Change the color of parent to
- black if read
- Double Black if black
- If still DB exit, then apply these cases.

- Case-4: if DB sibling is red.
- Swap colour of parent and its siblings
- Rotate parent in DB direction.
- Re-apply cases.

- Case-5: if DB sibling is black, one of its Sibling's child is Red
- Swap colour of parent & sibling.
- Rotate parent in DB direction.
- Remove DB.
- Change colour of Sibling's red child to black.
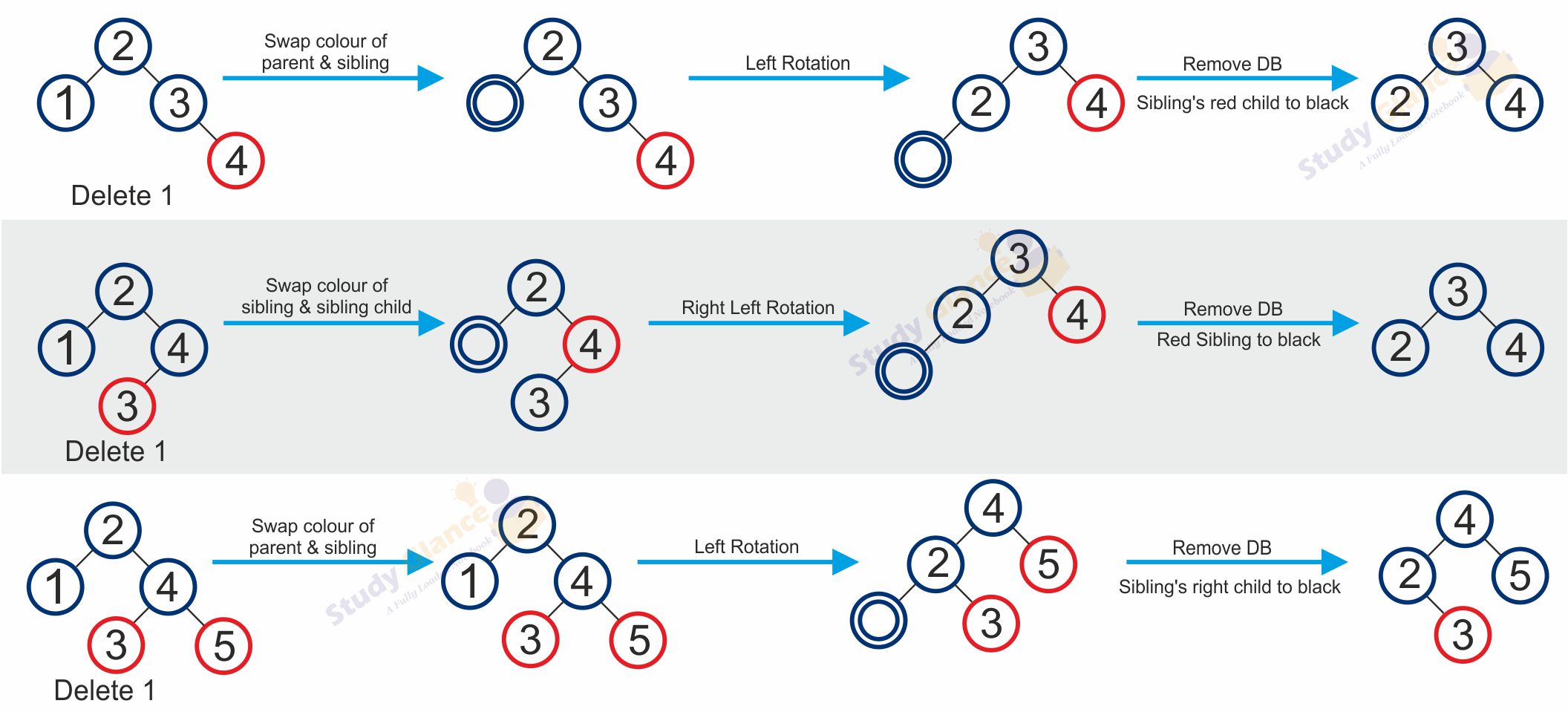
Algorithm for Deletion Operations of Red Black Tree
RB-DELETE(T, x)
BST-DELETE(T, x)
while x ≠ T.root and x.color == BLACK
if x == x.parent.left
s = x.parent.right
if s.color == RED
s.color = BLACK
x.parent.color = RED
LEFT-ROTATE(T, x.parent)
s = x.parent.right
if s.left.color == BLACK and s.right.color == BLACK
s.color = RED
x = x.parent
else if s.right.color == BLACK
s.left.color = BLACK
s.color = RED
RIGHT-ROTATE(T, s)
s = x.parent.right
s.color = x.parent.right
x.parent.color = BLACK
s.right.color = BLACK
LEFT-ROTATE(T, x.parent)
x = T.root
else (same as then close with “right” and “left” exchanged)
x.color = BLACKC Program to implement Red Black Tree
// Red Black Tree operations in C
#include <stdio.h>
#include <stdlib.h>
// Red-Black Tree Node Structure
typedef struct Node {
int data;
struct Node* parent;
struct Node* left;
struct Node* right;
int color; // 0 for black, 1 for red
} Node;
// Red-Black Tree Structure
typedef struct RedBlackTree {
Node* root;
} RedBlackTree;
// Create a new Red-Black Tree Node
Node* createNode(int data) {
Node* newNode = (Node*)malloc(sizeof(Node));
if (newNode == NULL) {
printf("Memory allocation error\n");
exit(1);
}
newNode->data = data;
newNode->parent = newNode->left = newNode->right = NULL;
newNode->color = 1; // New nodes are initially red
return newNode;
}
// Create a new Red-Black Tree
RedBlackTree* createRedBlackTree() {
RedBlackTree* newTree = (RedBlackTree*)malloc(sizeof(RedBlackTree));
if (newTree == NULL) {
printf("Memory allocation error\n");
exit(1);
}
newTree->root = NULL;
return newTree;
}
// Function to perform left rotation
void leftRotate(RedBlackTree* tree, Node* x) {
Node* y = x->right;
x->right = y->left;
if (y->left != NULL)
y->left->parent = x;
y->parent = x->parent;
if (x->parent == NULL)
tree->root = y;
else if (x == x->parent->left)
x->parent->left = y;
else
x->parent->right = y;
y->left = x;
x->parent = y;
}
// Function to perform right rotation
void rightRotate(RedBlackTree* tree, Node* y) {
Node* x = y->left;
y->left = x->right;
if (x->right != NULL)
x->right->parent = y;
x->parent = y->parent;
if (y->parent == NULL)
tree->root = x;
else if (y == y->parent->left)
y->parent->left = x;
else
y->parent->right = x;
x->right = y;
y->parent = x;
}
// Function to fix the Red-Black Tree properties after insertion
void insertFixup(RedBlackTree* tree, Node* z) {
while (z->parent != NULL && z->parent->color == 1) {
if (z->parent == z->parent->parent->left) {
Node* y = z->parent->parent->right;
if (y != NULL && y->color == 1) {
z->parent->color = 0; // Black
y->color = 0; // Black
z->parent->parent->color = 1; // Red
z = z->parent->parent;
} else {
if (z == z->parent->right) {
z = z->parent;
leftRotate(tree, z);
}
z->parent->color = 0; // Black
z->parent->parent->color = 1; // Red
rightRotate(tree, z->parent->parent);
}
} else {
Node* y = z->parent->parent->left;
if (y != NULL && y->color == 1) {
z->parent->color = 0; // Black
y->color = 0; // Black
z->parent->parent->color = 1; // Red
z = z->parent->parent;
} else {
if (z == z->parent->left) {
z = z->parent;
rightRotate(tree, z);
}
z->parent->color = 0; // Black
z->parent->parent->color = 1; // Red
leftRotate(tree, z->parent->parent);
}
}
}
tree->root->color = 0; // Root must be black
}
// Function to insert a node into the Red-Black Tree
void insert(RedBlackTree* tree, int data) {
Node* z = createNode(data);
Node* y = NULL;
Node* x = tree->root;
while (x != NULL) {
y = x;
if (z->data < x->data)
x = x->left;
else
x = x->right;
}
z->parent = y;
if (y == NULL)
tree->root = z;
else if (z->data < y->data)
y->left = z;
else
y->right = z;
insertFixup(tree, z);
}
// Function to find the minimum value node in the tree rooted at a given node
Node* findMinValueNode(Node* node) {
Node* current = node;
while (current->left != NULL)
current = current->left;
return current;
}
// Function to fix the Red-Black Tree properties after deletion
void deleteFixup(RedBlackTree* tree, Node* x) {
while (x != tree->root && x->color == 0) {
if (x == x->parent->left) {
Node* w = x->parent->right;
if (w->color == 1) {
w->color = 0; // Black
x->parent->color = 1; // Red
leftRotate(tree, x->parent);
w = x->parent->right;
}
if (w->left->color == 0 && w->right->color == 0) {
w->color = 1; // Red
x = x->parent;
} else {
if (w->right->color == 0) {
w->left->color = 0; // Black
w->color = 1; // Red
rightRotate(tree, w);
w = x->parent->right;
}
w->color = x->parent->color;
x->parent->color = 0; // Black
w->right->color = 0; // Black
leftRotate(tree, x->parent);
x = tree->root;
}
} else {
Node* w = x->parent->left;
if (w->color == 1) {
w->color = 0; // Black
x->parent->color = 1; // Red
rightRotate(tree, x->parent);
w = x->parent->left;
}
if (w->right->color == 0 && w->left->color == 0) {
w->color = 1; // Red
x = x->parent;
} else {
if (w->left->color == 0) {
w->right->color = 0; // Black
w->color = 1; // Red
leftRotate(tree, w);
w = x->parent->left;
}
w->color = x->parent->color;
x->parent->color = 0; // Black
w->left->color = 0; // Black
rightRotate(tree, x->parent);
x = tree->root;
}
}
}
x->color = 0; // Black
}
// Function to delete a node from the Red-Black Tree
void delete(RedBlackTree* tree, int data) {
Node* z = tree->root;
while (z != NULL) {
if (data == z->data) {
Node* y = z;
Node* x;
int yOriginalColor = y->color;
if (z->left == NULL) {
x = z->right;
transplant(tree, z, z->right);
} else if (z->right == NULL) {
x = z->left;
transplant(tree, z, z->left);
} else {
y = findMinValueNode(z->right);
yOriginalColor = y->color;
x = y->right;
if (y->parent == z) {
if (x != NULL)
x->parent = y;
} else {
transplant(tree, y, y->right);
y->right = z->right;
if (y->right != NULL)
y->right->parent = y;
}
transplant(tree, z, y);
y->left = z->left;
y->left->parent = y;
y->color = z->color;
}
free(z);
if (yOriginalColor == 0)
deleteFixup(tree, x);
return;
} else if (data < z->data)
z = z->left;
else
z = z->right;
}
}
// Transplant the subtree rooted at node u with the subtree rooted at node v
void transplant(RedBlackTree* tree, Node* u, Node* v) {
if (u->parent == NULL)
tree->root = v;
else if (u == u->parent->left)
u->parent->left = v;
else
u->parent->right = v;
if (v != NULL)
v->parent = u->parent;
}
// Function to perform in-order traversal of the Red-Black Tree
void inOrderTraversal(Node* root) {
if (root != NULL) {
inOrderTraversal(root->left);
printf("%d ", root->data);
inOrderTraversal(root->right);
}
}
// Function to free memory by deallocating nodes
void freeMemory(Node* root) {
if (root == NULL)
return;
freeMemory(root->left);
freeMemory(root->right);
free(root);
}
int main() {
int choice,value;
RedBlackTree* tree = createRedBlackTree();
do
{
printf("1. Insertion\n2. Deletion\n3. Display\n4. Exit");
printf("\nEnter your choice: ");
scanf("%d",&choice);
switch(choice)
{
case 1: printf("Enter the value to be insert: ");
scanf("%d",&value);
insert(tree, value);
break;
case 2: printf("Enter the value to be deleted: ");
scanf("%d",&value);
delete(tree, value);
break;
case 3: inOrderTraversal(tree->root);
break;
case 4: freeMemory(tree->root);
break;
default: printf("\nWrong selection!!! Try again!!!");
}
}while(choice!=4);
return(0);
} Next Topic :Splay Tree
