DS Menu

B Tree

B-Trees were introduced by Rudolf Bayer and Edward M. McCreight at Boeing Research Labs in 1970 with the name Height Balanced M-way Search Tree. Later it was named as B-Tree. A B-tree is a self-balancing tree where all the leaf nodes are at the same level which allows for efficient searching, insertion and deletion of records. Because of all the leaf nodes being on the same level, the access time of data is fixed regardless of the size of the data set.

In binary search tree, AVL Tree, Red-Black tree, etc., every node contains only one value(key) and a maximum of two children. B-Tree contains more than one value and more than two children. The number of values(keys) in a node and number of childrens for a node is called as order of B-Tree.

Properties of B-Tree of Order m

All leaf nodes must be at same level.
All nodes except root should have at least m/2 - 1 keys.
All non leaf nodes except root should have at least m/2 children.
If the root node is a non leaf node, then it must have atleast 1 key.
A non leaf node with m-1 keys must have m number of children.
All keys of each node of a B tree, should be stored in the ascending order.

Algorithm or Pseudocode for Searching an Element in a B-Tree

Pseudo-code

function search(node, key):
    i = 1
    while i <= node.n and key > node.keys[i]:
        i = i + 1
    if i <= node.n and key == node.keys[i]:
        return (node, i)  // Key found
    else if node.leaf:
        return null       // Key not found and reached leaf
    else:
        return search(node.children[i], key) // Go to the appropriate child

Insertion operation in B-Tree

Here's a step-by-step explanation of the insertion process in a B-tree:

Case 0: Start at the Root
- If tree is Empty, then create a new node with key value and make as a root node.
- If the tree is not Empty, traverse down the tree from the root to the appropriate leaf node where the new key should be inserted. The correct node is determined by comparing the key to be inserted with the keys in each node and following the correct child pointer.
Case 1: Inserting into a Non-Full Leaf Node
- If the leaf node has less than m-1 keys, Insert the key into the node in its correct sorted position.
Case 2: Inserting into a Full Leaf Node (If the leaf node is full, it must be split before the new key is inserted.)
- Create a new node.
- Distribute keys evenly between the original and new nodes, keeping the median key in the parent node and make parent node as root.
- Insert the new key into the appropriate node.
- If the parent node is also full, recursively apply Case 2 to the parent until a non-full node is reached.

Insert the elements 5, 50, 30, 80, 90, 60, and 65 into B-Tree with an order 3

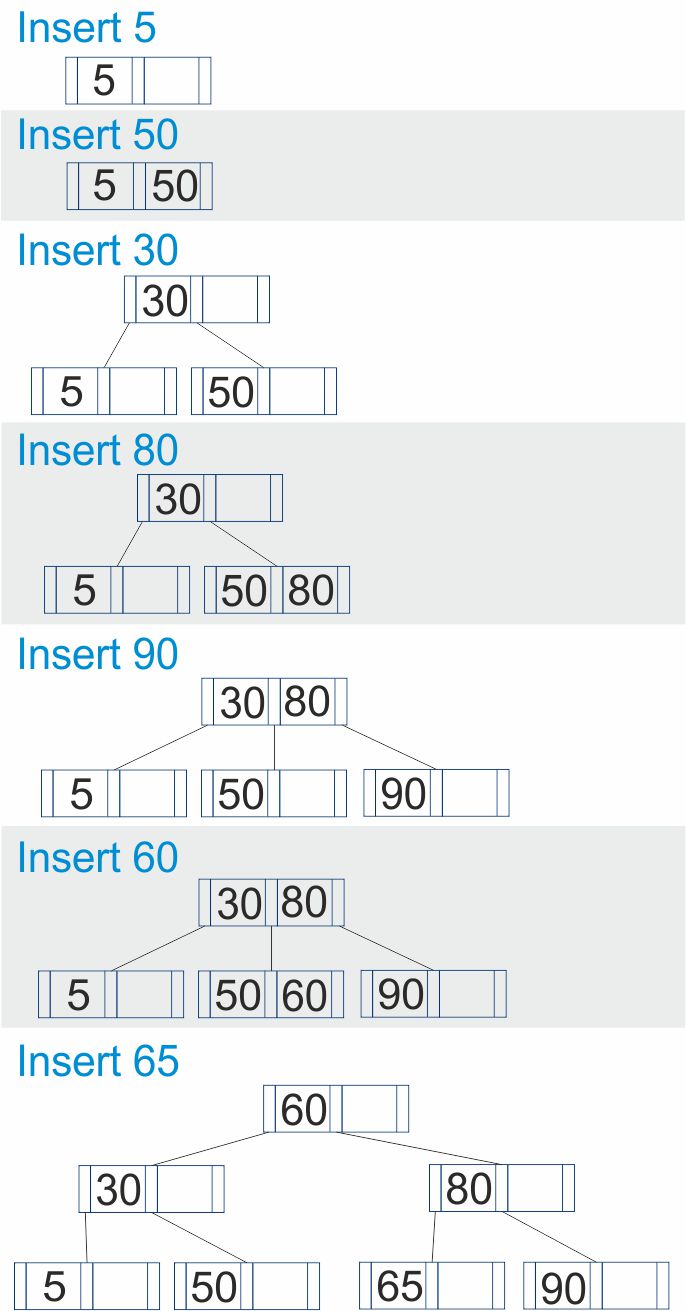
Algorithm or Pseudocode for Inserting an Element in a B-Tree

Pseudo-code

function insert(tree, key):
    root = tree.root
    if root.n == m-1:
        newNode = createNode()
        tree.root = newNode
        newNode.leaf = false
        newNode.n = 0
        newNode.children[1] = root
        splitChild(newNode, 1)
        insertNonFull(newNode, key)
    else:
        insertNonFull(root, key)

function insertNonFull(node, key):
    i = node.n
    if node.leaf:
        while i >= 1 and key < node.keys[i]:
            node.keys[i + 1] = node.keys[i]
            i = i - 1
        node.keys[i + 1] = key
        node.n = node.n + 1
    else:
        while i >= 1 and key < node.keys[i]:
            i = i - 1
        i = i + 1
        if node.children[i].n == m-1:
            splitChild(node, i)
            if key > node.keys[i]:
                i = i + 1
        insertNonFull(node.children[i], key)

function splitChild(node, i):
    newNode = createNode()
    newNode.leaf = node.children[i].leaf
    newNode.n = t-1
    for j = 1 to t-1:
        newNode.keys[j] = node.children[i].keys[j+t]
    if not node.children[i].leaf:
        for j = 1 to t:
            newNode.children[j] = node.children[i].children[j+t]
    node.children[i].n = t-1
    for j = node.n + 1 downto i+1:
        node.children[j+1] = node.children[j]
    node.children[i+1] = newNode
    for j = node.n downto i:
        node.keys[j+1] = node.keys[j]
    node.keys[i] = node.children[i].keys[t]
    node.n = node.n + 1

Delete Operation in B-Tree

When deleting, you have to make sure that the B tree properties are preserved. We consider 3 cases in deletion of B trees.

Case 1: Key is in a Leaf Node(with Sufficient Keys)

If the key k is in a leaf node N and N has more than the minimum number of keys, simply remove k from N.

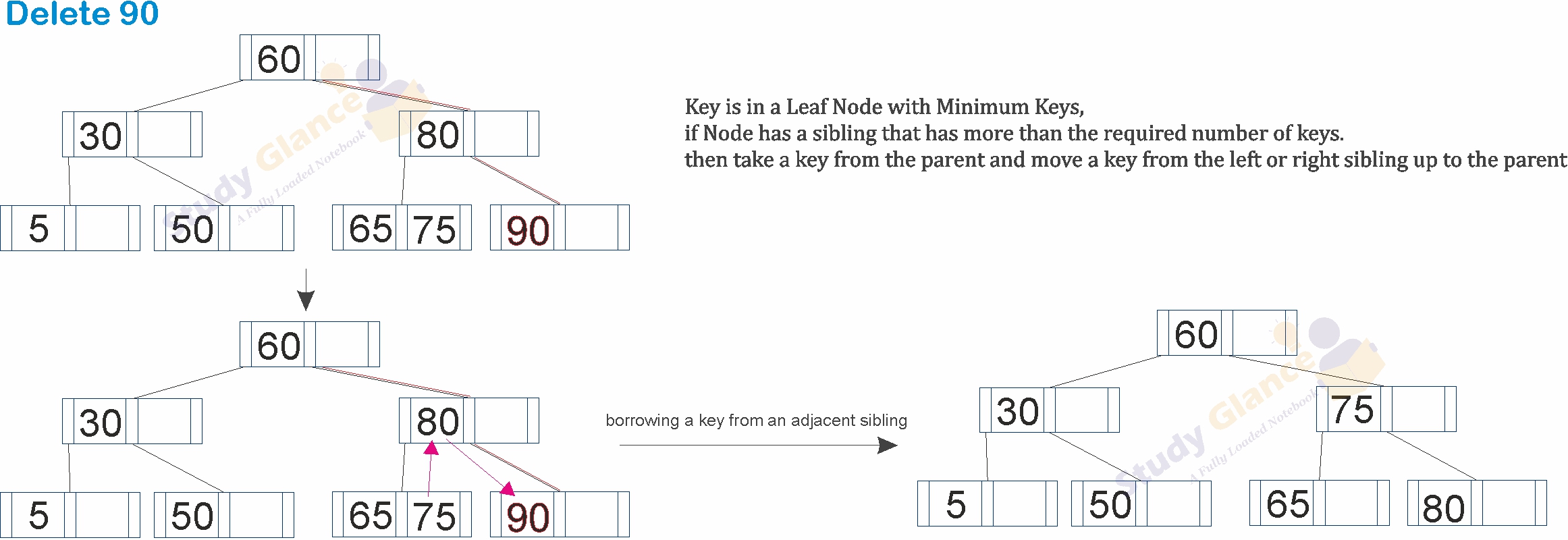
Case 2: Key is in a Leaf Node(with Minimum Keys would violate the B-tree property)

The leaf has a sibling that has more than the required number of keys.
- we can take a key from the parent and move a key from the left or right sibling up to the parent(borrowing a key from an adjacent sibling).
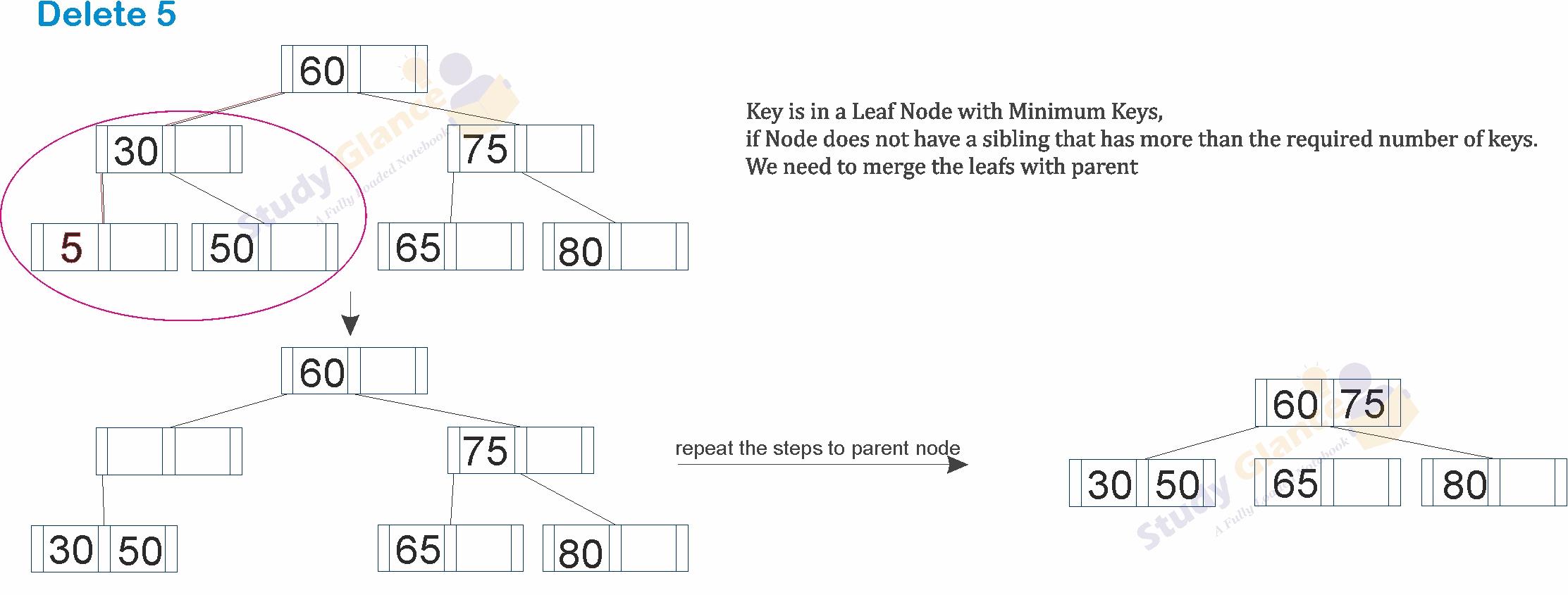
The leaf does not have a sibling that has more than the required number of keys.
- We need to merge the leaf with either its left or right sibling.
- Because two leaves are being merged, we also need to take the key from the parent whose left and right pointers used to point to these two leaves and add this key to the merged node.

Case 3: Key is in an Internal Node

Key in an Internal Node with a Child Having More than the Minimum Keys.
- If the key k is in an internal node N, find the predecessor k₀ of k in the subtree rooted at the left child of k. Replace k with k₀ and then delete k₀ from the left child.
- If the left child has only the minimum number of keys, then can be done with the successor in the right subtree.
Key in an Internal Node with Children Having Only Minimum Keys.
- If both immediate children of the internal node N that contains k have the minimum number of keys, merge these children along with k. Then delete k from the merged node.

Note: If the Root is Left with No Keys, delete the old root and make its only child the new root of the tree. This decreases the height of the tree.

Algorithm or Pseudocode for Deleting an Element in a B-Tree

Pseudo-code

function delete(tree, key):
    if tree.root is None:
        print("Tree is empty.")
        return

    // Call the delete procedure for the root
    deleteNode(tree.root, key)

    // If the root node has 0 keys, make its first child the new root
    // if it has a child, otherwise set the root to None.
    if tree.root.n == 0:
        if tree.root.leaf:
            tree.root = None
        else:
            tree.root = tree.root.children[0]

function deleteNode(node, key):
    i = findKey(node, key)

    // Case 1: The key to be removed is present in this node
    if i <= node.n and node.keys[i] == key:
        if node.leaf:
            // The node is a leaf node: Remove the key directly
            removeFromLeaf(node, i)
        else:
            // The node is an internal node
            removeFromNonLeaf(node, i)
    else:
        if node.leaf:
            // The key is not present in tree
            print("The key", key, "is does not exist in the tree")
            return

        // The key might be present in the subtree rooted at this node
        // The flag indicates whether the key is present in the subtree
        // rooted at the last child of this node
        flag = (i == node.n)

        // If the child where the key is supposed to exist has less than t keys,
        // we fill that child
        if node.children[i].n < t:
            fill(node, i)

        // If the last child has been merged, it must have merged with the previous
        // child and so we recurse on the (i-1)th child. Else, we recurse on the
        // (i)th child which now has atleast t keys
        if flag and i > node.n:
            deleteNode(node.children[i-1], key)
        else:
            deleteNode(node.children[i], key)

// A utility function to remove the ith key from this node - which is a leaf node
function removeFromLeaf(node, i):
    // Move all the keys after the ith position one place backward
    for j in range(i+1, node.n):
        node.keys[j-1] = node.keys[j]

    // Reduce the count of keys
    node.n -= 1

// A utility function to remove the ith key from this node - which is a non-leaf node
function removeFromNonLeaf(node, i):
    key = node.keys[i]

    // If the child that precedes key in this node has atleast t keys,
    // find the predecessor 'pred' of key in the subtree rooted at
    // child[i]. Replace key by pred. Recursively delete pred
    // in children[i]
    if node.children[i].n >= t:
        pred = getPred(node, i)
        node.keys[i] = pred
        deleteNode(node.children[i], pred)

    // If the child[i] has less that t keys, examine child[i+1].
    // If child[i+1] has atleast t keys, find the successor 'succ' of key in
    // the subtree rooted at child[i+1]
    // Replace key by succ
    // Recursively delete succ in child[i+1]
    else if node.children[i+1].n >= t:
        succ = getSucc(node, i)
        node.keys[i] = succ
        deleteNode(node.children[i+1], succ)

    // If both child[i] and child[i+1] has less than t keys,merge key and all of child[i+1]
    // into child[i]
    // Now child[i] contains 2t-1 keys
    // Free child[i+1] and recursively delete key from child[i]
    else:
        merge(node, i)
        deleteNode(node.children[i], key)

// A function to get predecessor of keys[i]
function getPred(node, i):
    // Keep moving to the right most node until we reach a leaf
    current = node.children[i]
    while not current.leaf:
        current = current.children[current.n]

    // Return the last key of the leaf
    return current.keys[current.n-1]

// A function to get successor of keys[i]
function getSucc(node, i):
    // Keep moving the left most node starting from child[i+1] until we reach a leaf
    current = node.children

Next Topic :B+ Tree