DS Menu

Splay Tree

The splay tree was developed by Daniel Dominic Sleator and Robert Endre Tarjan in 1985. A Splay Tree is a self-adjusting binary search tree data structure that automatically reorganizes itself to optimize access times for frequently accessed elements by moving them closer to the root. It accomplishes this by performing a splay operation after every search, insert, or delete operation, bringing the accessed node to the root of the tree.

Key Features of Splay Trees

Self-Adjusting: After any operation, the accessed node is splayed to the root of the tree, making it the new root. This helps improve the access time for frequently accessed elements.
No Height Balance Guarantee: Unlike AVL trees and Red-Black trees, Splay Trees do not guarantee a balanced height. However, they exhibit a form of local balance, which means nodes that are frequently accessed tend to move closer to the root.

Splay Tree Rotations:

Splay Trees use rotations to perform the splay operation and bring the accessed node to the root.

Zig Rotation(Right)

This rotation moves a child node up and its parent node down, making the child the new parent.
It is used when the target node is the right child of its parent.

Zag Rotation(Left)

Similar to the zig rotation, the zag rotation moves a child node up and its parent node down, but the child becomes the left child of the new parent.
It is used when the target node is the left child of its parent

Zig – Zig Rotation

In a Zig-Zig rotation, two consecutive rotations are performed to move a node up two levels closer to the root.
The first rotation moves the target node's grandchild up and its child down.
The second rotation moves the target node up and its previous grandchild down.
It is used when the target node is the right child of the right child of its parent.

Zag – Zag Rotation

In a Zag-Zag rotation, two consecutive rotations are performed to move a node up two levels closer to the root.
This rotation is similar to the zig-zig rotation but involves two consecutive zag rotations.
It is used when the target node is the left child of the left child of its parent.

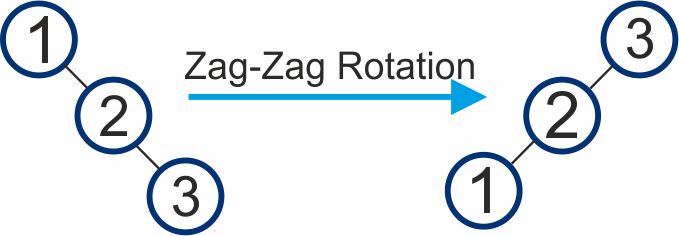
Zig – Zag Rotation

In a Zig-Zag rotation, two consecutive rotations are performed to move a node up one level closer to the root.
This rotation combines a zig rotation followed by a zag rotation.
It is used when the target node is the right child of the left child of its parent.

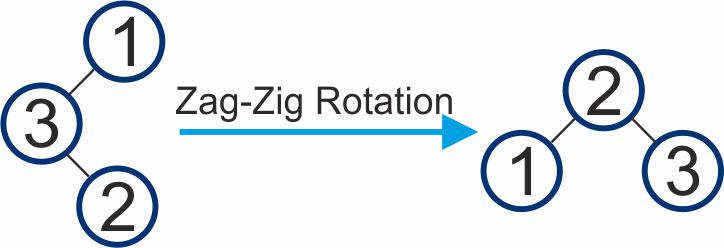
Zag – Zig Rotation

In a Zag-Zig rotation, two consecutive rotations are performed to move a node up one level closer to the root.
This rotation performs a zag rotation followed by a zig rotation.
It is used when the target node is the left child of the right child of its parent.

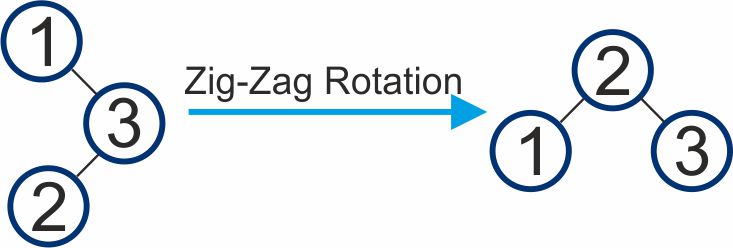
Insertion in a Splay Tree:

Pseudocode

procedure splayInsert(root, key):
    if root is null:
        // Create a new node with the given key and make it the root
        root = createNode(key)
    else:
        // Perform a normal BST insertion
        root = bstInsert(root, key)
    
    // Splay the newly inserted node to the root
    root = splay(root, key)

function bstInsert(node, key):
    // Standard BST insertion procedure
    if node is null:
        return createNode(key)
    if key < node.key:
        node.left = bstInsert(node.left, key)
    else if key > node.key:
        node.right = bstInsert(node.right, key)
    return node

function splay(root, key):
    if root is null or root.key == key:
        return root
    
    // Key is in the left subtree
    if key < root.key:
        // Key is not in the tree, return the unchanged root
        if root.left is null:
            return root
        // Zig-Zig step: Left-left case
        if key < root.left.key:
            root.left.left = splay(root.left.left, key)
            root = rightRotate(root)
        // Zig-Zag step: Left-right case
        else if key > root.left.key:
            root.left.right = splay(root.left.right, key)
            if root.left.right is not null:
                root.left = leftRotate(root.left)
        // Perform a final rotation to bring the key to the root
        if root.left is not null:
            root = rightRotate(root)
        return root
    
    // Key is in the right subtree
    else:
        // Key is not in the tree, return the unchanged root
        if root.right is null:
            return root
        // Zig-Zig step: Right-right case
        if key > root.right.key:
            root.right.right = splay(root.right.right, key)
            root = leftRotate(root)
        // Zig-Zag step: Right-left case
        else if key < root.right.key:
            root.right.left = splay(root.right.left, key)
            if root.right.left is not null:
                root.right = rightRotate(root.right)
        // Perform a final rotation to bring the key to the root
        if root.right is not null:
            root = leftRotate(root)
        return root

function rightRotate(node):
    // Right rotation operation
    newRoot = node.left
    node.left = newRoot.right
    newRoot.right = node
    return newRoot

function leftRotate(node):
    // Left rotation operation
    newRoot = node.right
    node.right = newRoot.left
    newRoot.left = node
    return newRoot

Deletion in a Splay Tree:

Pseudocode

procedure splayDelete(root, key):
    if root is null:
        // Key not found, return the unchanged root
        return root
    
    // Splay the node containing the key to the root
    root = splay(root, key)
    
    // After splaying, if the key is not at the root, it's not in the tree
    if key != root.key:
        return root
    
    // Perform the actual deletion
    if root.left is null:
        return root.right
    else:
        // Find the maximum node in the left subtree
        maxNode = findMax(root.left)
        // Splay the maximum node to the root of the left subtree
        root.left = splay(root.left, maxNode.key)
        // Attach the right subtree as the right child of the maximum node
        maxNode.right = root.right
        return maxNode

function findMax(node):
    // Find the maximum node in a subtree
    while node.right is not null:
        node = node.right
    return node

Searching in a Splay Tree

Pseudocode

function splaySearch(root, key):
    if root is null:
        // Key not found, return null or a sentinel value
        return null
    
    // Start searching from the root
    while root is not null:
        if key == root.key:
            // Key found, splay the node to the root
            return splay(root, key)
        else if key < root.key:
            // Key is in the left subtree
            if root.left is null:
                // Key not found, splay the last accessed node (root)
                return splay(root, key)
            // Continue searching in the left subtree
            root = root.left
        else:
            // Key is in the right subtree
            if root.right is null:
                // Key not found, splay the last accessed node (root)
                return splay(root, key)
            // Continue searching in the right subtree
            root = root.right
    
    // Key not found, return null or a sentinel value
    return null

Next Topic :B Tree