DS Menu

B+ Tree

A B+ tree is a self-balancing tree data structure that keeps data sorted and allows for efficient search, insertion, and deletion operations. It is often used in databases and file systems to organize and access large amounts of data.

B+ Trees retain the basic principles of B-Trees but introduce significant modifications that enhance performance in disk-based storage systems. These modifications include storing all data in leaf nodes and linking these leaf nodes to facilitate efficient sequential access, which is particularly valuable for range queries.

Properties or Characteristics of B+ Trees

In a B+ Tree, all data records are stored at the leaf level. This contrasts with a B-tree, where data can be at any level.
Leaf nodes in a B+ Tree are linked together in a linked list fashion, facilitating efficient range queries and sequential access.
The internal nodes (non-leaf nodes) of a B+ Tree do not store data. Instead, they act as indexes containing only keys that guide the search towards the leaf nodes.
Due to the high degree (number of child pointers per node), B+ Trees are typically shallower than B-trees with the same number of elements. This results in fewer disk reads, which is crucial for performance in disk-based storage.
All leaf nodes are at the same depth, which ensures that every access path from the root to a leaf node is of the same length, providing consistent query performance.
By storing values only in leaves and maintaining a high fan-out, B+ Trees use disk space more efficiently and reduce the number of disk I/O operations needed.
Like B-trees, B+ Trees are self-balancing. Insertions and deletions may cause redistribution of keys among nodes or splitting/merging of nodes but maintain the tree's balance.

B+ Tree Insertion in data structure

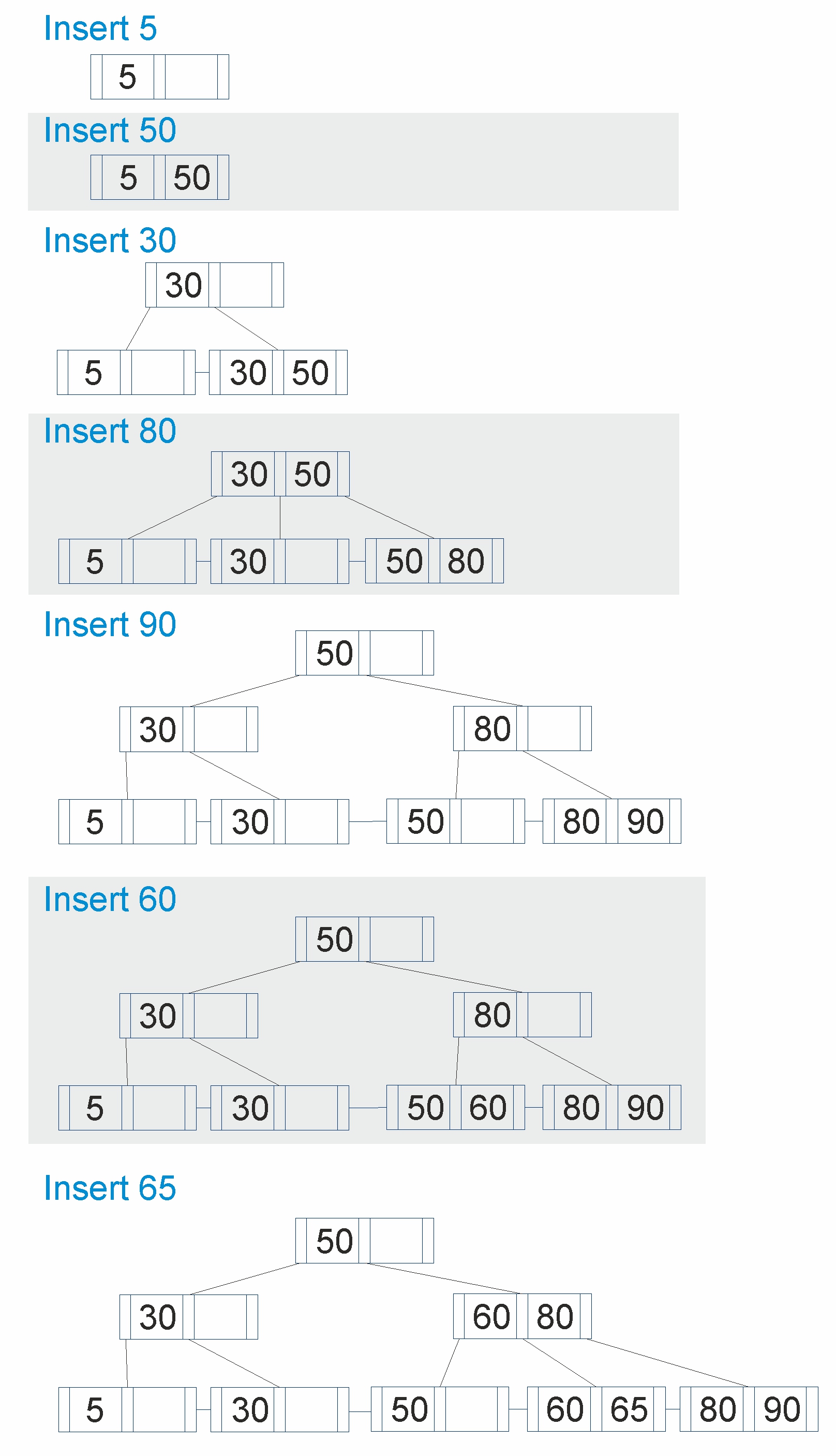
Case 1: Inserting into a Non-Full Leaf Node
- If the leaf node has less than m-1 keys, Insert the key into the node in its correct sorted position.
Case 2: Inserting into a Full Leaf Node (If the leaf node is full, it must be split before the new key is inserted.)
- Create a new leaf node.
- Distribute keys evenly between the original and new nodes, keeping the median key in the original node.
- Insert the new key into the appropriate node.
- Promote the median key to the parent node and make it root.
- Update sibling pointers to maintain linked leaf structure.
- If the parent node is also full, recursively apply Case 2 to the parent until a non-full node is reached.

Insert the elements 5, 50, 30, 80, 90, 60, and 65 into B+ Tree with an order 3

Difference between B-Tree and B+ trees

Feature	B-Tree	B+ Tree
Node Structure	All nodes, including leaf nodes, can store both keys and data. Internal nodes also contain pointers to their child nodes.	Only leaf nodes store data, while internal nodes only contain keys and pointers to child nodes.
Linked Leaf Nodes	Leaf nodes are not linked to each other.	Leaf nodes are linked together in a doubly linked list, allowing efficient range searches.
Key Distribution	Keys are distributed throughout all nodes, including internal nodes.	Keys are only stored in leaf nodes, allowing for a more balanced distribution of keys across the tree.
Search Performance	Search requires traversing the tree from the root to the leaf node containing the desired key.	Search only involves traversing the leaf nodes using the linked list, leading to potentially faster search performance for range searches.
Insertion and Deletion	Insertion and deletion can occur in both internal and leaf nodes, requiring splitting or merging nodes to maintain balance.	Insertion and deletion occur only in leaf nodes, simplifying the process and potentially reducing overhead.
Space Utilization	Internal nodes store both keys and data, leading to lower space utilization in large trees.	Internal nodes only store keys, allowing for more efficient space utilization, especially in memory-constrained environments.
Write Performance	Frequent insertions and deletions can lead to more frequent node splits and merges, potentially impacting write performance.	Localized insertions and deletions in leaf nodes can improve write performance compared to B-trees.
Applications	Suitable for applications where data access patterns are random and range searches are not crucial.	Ideal for applications requiring efficient range searches, such as databases, file systems, and search engines.

Next Topic :Comparison of Trees