Data Structures - Introduction
- Abstract data types
- Linear Data Structures
- Linked List Introduction
- Single Linked List
- Stacks using Array
- Stacks using linkedlist
- Queues using array
- Queues using linkedlist
- Stack Applications
- Infix to Postfic Converstion
- Postfix Evaluation
- Dictionaries
- Introduction to Dictionaries
- Linear list representation
- Skip list representation
- Hash Table
- Introduction Hash Table
- Hash functions
- Collision Resolution
- Separate chaining
- Open addressing
- Rehashing
- Extendible hashing
- Trees
- Introduction to Tree
- Binary trees Representation
- Binary tree traversals
- Binary Search Tree
- AVL Tree
- Red Black Tree
- Splay Tree
- B Tree
- B+ Tree
- Comparison of Trees
- Graphs
- Introduction to Graph
- Graph Representation
- Breadth-First Search
- Depth-First Search
- Sorting
- Quick Sort
- Merge Sort
- Heap Sort
- Pattern Matching
- Introduction to pattern Matching
- Brute force Pattern Matching
- Boyer–Moore Pattern Matching
- KMP Pattern Matching
- Tries
- Introduction to Tries
- Standard Trie
- Compressed tries
- Suffix Trie
Introduction to Graph
Definition of Graph
A graph, in the context of mathematics and computer science, is a data structure used to represent relationships between entities. It consists of two sets:
- Vertices (V): Represent the entities themselves, also called nodes or points.
- Edges (E): Represent the relationships between the entities, also called links or lines.
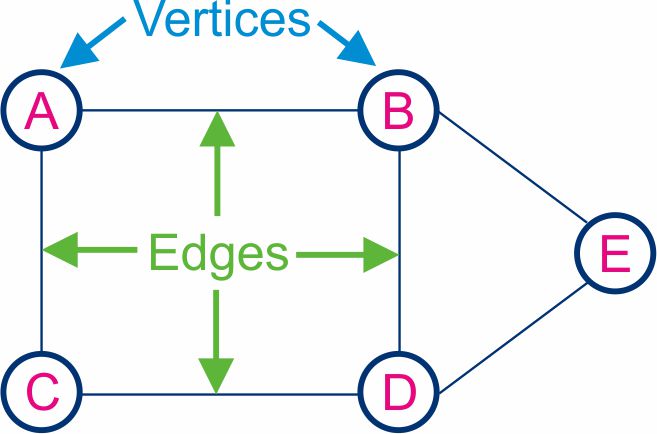
A graph is denoted as G = (V, E), where:
-V is a set of vertices.
-E is a set of edges.
These edges can be directed or undirected:
- Directed edges: Have an arrow indicating direction, showing how one vertex connects to another (e.g., A → B).
- Undirected edges: Have no direction, representing a bi-directional connection between two vertices (e.g., A - B).
Graph Terminology
- Graph: A collection of nodes (or vertices) and edges that connect pairs of nodes.
- Vertex (Node): The fundamental unit by which graphs are formed. A vertex represents a point in the graph.
- Edge: A line connecting two vertices in a graph. It can be directed (having a direction) or undirected (no direction).
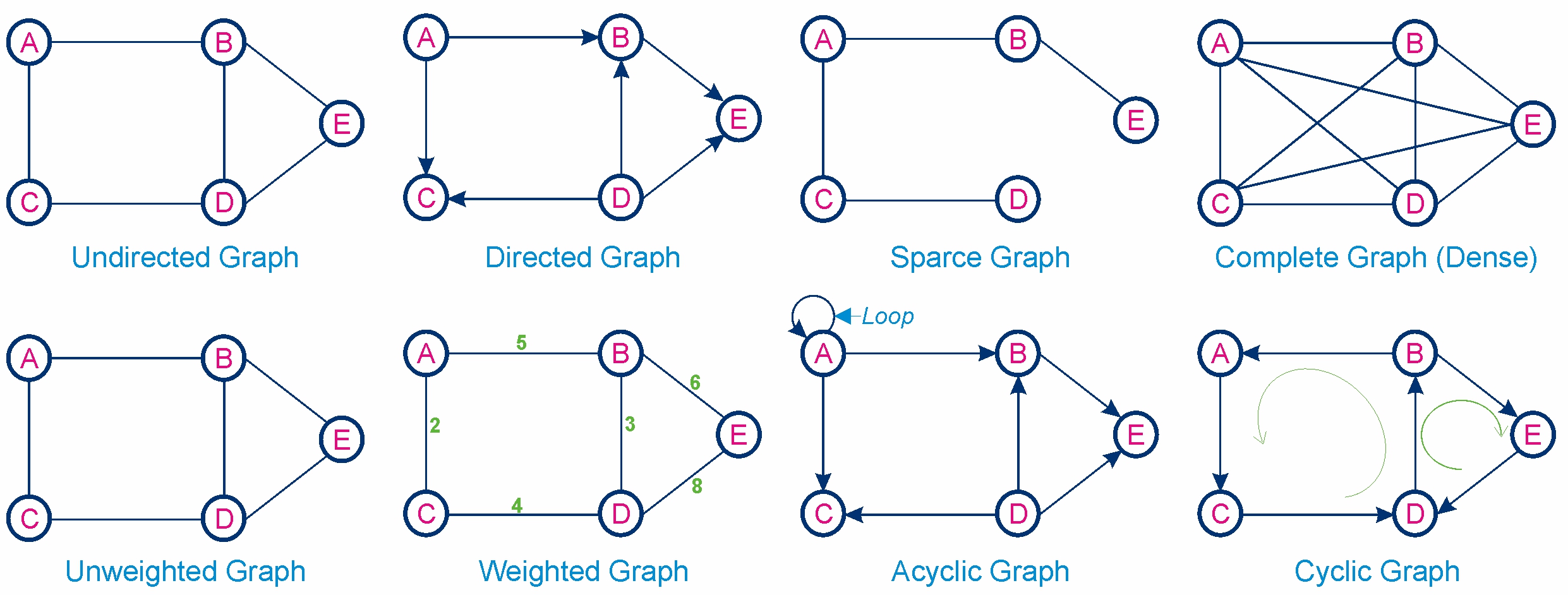
- Directed Graph (Digraph): A graph in which the edges have a direction, indicating a one-way relationship between vertices.
- Undirected Graph: A graph in which the edges do not have a direction, indicating a two-way relationship.
- Weighted Graph: A graph in which edges have weights assigned to them, typically representing costs, lengths, or capacities.
- Unweighted Graph: A graph in which edges do not have weights.
- Adjacent (Neighbors): Two vertices are adjacent if there is an edge connecting them.
- Degree: The degree of a vertex is the number of edges connected to it. For directed graphs, there are in-degree (edges coming into the vertex) and out-degree (edges going out from the vertex).
- Path: A sequence of edges that allows you to go from one vertex to another.
- Cycle: A path that starts and ends at the same vertex without traversing any edge more than once.
- Loop: An edge that connects a vertex to itself.
- Subgraph: A graph formed from a subset of the vertices and edges of another graph.
- Connected Graph: An undirected graph is connected if there is a path between every pair of vertices.
- Disconnected Graph: A graph is disconnected if it is not connected, i.e., if there are at least two vertices with no path between them.
- Complete Graph: A graph in which there is an edge between every pair of vertices.
- Bipartite Graph: A graph whose vertices can be divided into two disjoint sets such that every edge connects a vertex in one set to a vertex in the other set.
- Tree: A connected, undirected graph with no cycles.
- Acyclic Graph: A graph with no cycles. In the context of directed graphs, it is often called a Directed Acyclic Graph (DAG).
- Graph Isomorphism: Two graphs are isomorphic if there is a one-to-one correspondence between their vertex sets that preserves edge connectivity.
Next Topic :Graph Representation