Boyer–Moore Pattern Matching

The Boyer–Moore Pattern Matching algorithm is one of the most efficient string-searching algorithm that is the standard benchmark for practical pattern matching. It was developed by Robert Stephen Boyer and J Strother Moore in the year 1977.

The Boyer-Moore algorithm works by pre-processing the pattern and then scanning the text from right to left, starting with the rightmost characters. It is based on the principle that if a mismatch is found, there is no need to match the remaining characters. This backwards approach significantly reduces the algorithm's time complexity compared to naive string search methods.

Here's a step-by-step explanation of how the Boyer-Moore algorithm works:

1. Preprocessing

Boyer-Moore algorithm uses two heuristics for preprocessing the pattern:
a. Bad Character Heuristic
b. Good Suffix Heuristic

Bad Character Heuristic (Building Bad Character Table)

Determines how far the pattern can be shifted when a character mismatch occurs.

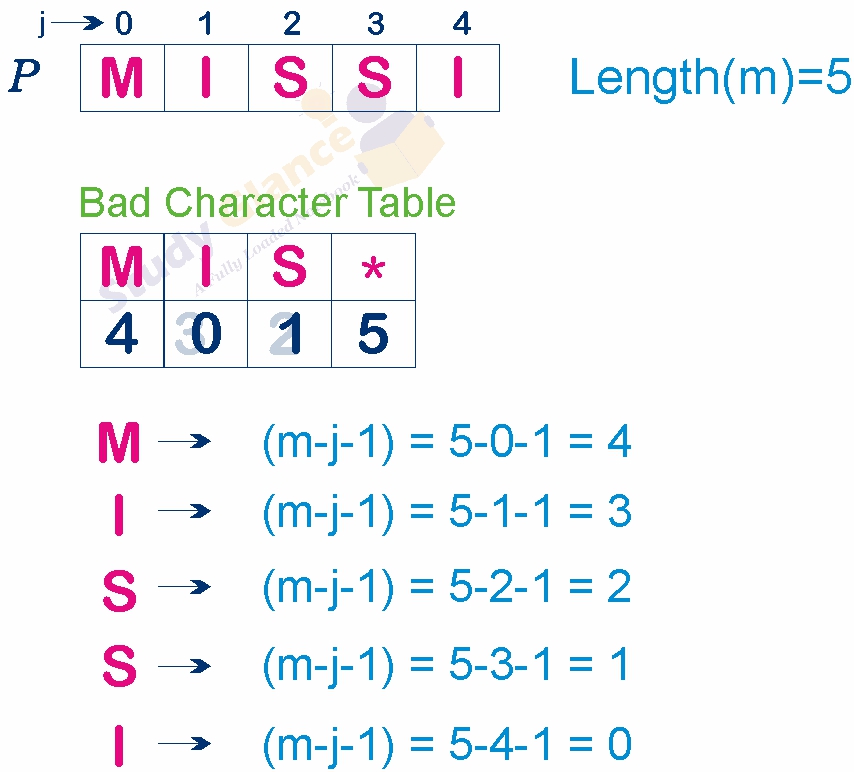
1. Create an array (often called the "Bad Character Table") to store the rightmost occurrence of each character in the pattern. If a character is not in the pattern, its value is set to pattern length.
2. For each character in the pattern, update the table with its last occurrence in the pattern with
   pattern length - index - 1.

Example:

2. Searching

Once the preprocessing is done, the actual search begins:

1. Align the pattern with the beginning of the text.
2. Compare the pattern with the text from right to left.
3. If all characters of the pattern match, a valid occurrence is found.

3. Shifting the Pattern:

When a mismatch occurs

• If the character is not in the pattern: Shift the pattern such that the mismatched character in the text aligns with the rightmost occurrence of it in the pattern.
• If the character is not in the pattern: shift the entire pattern past the character.

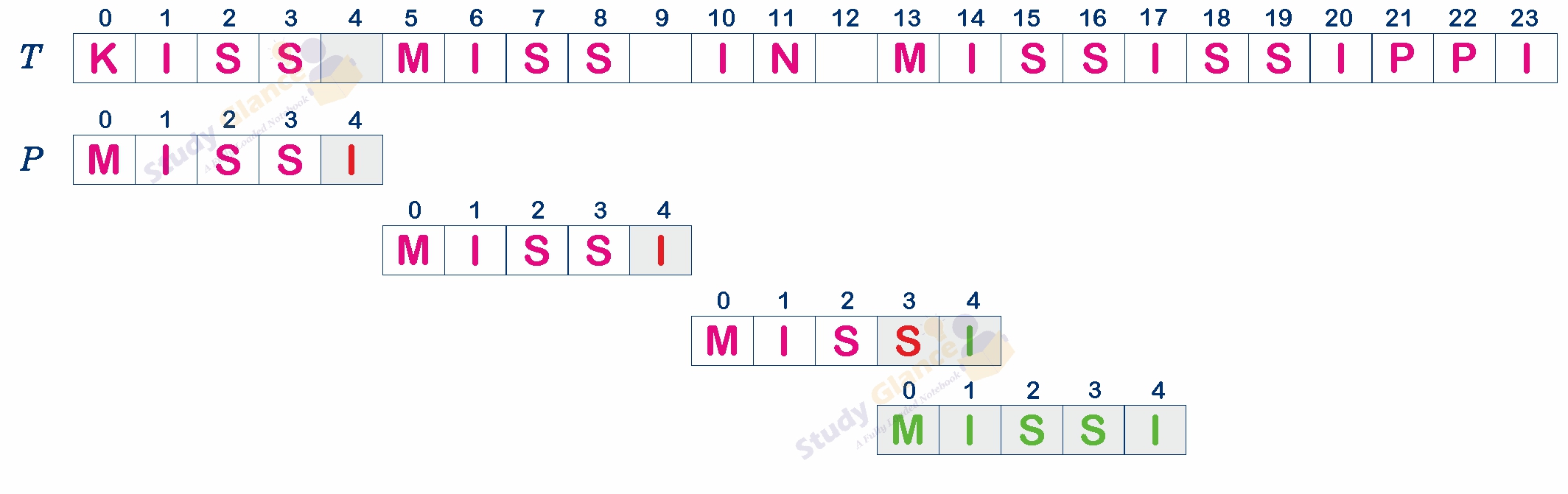
3. Repeat Comparison

After shifting the pattern according to the above rules, repeat the comparison process:

1. Continue comparing the pattern with the text from right to left.
2. Apply the shifting rules whenever a mismatch is encountered.
3. Continue this process until the end of the text is reached or all occurrences of the pattern are found.

4. Termination

The algorithm terminates when either

• The pattern has been shifted past the end of the text, indicating no more matches are possible.
• All occurrences of the pattern has have been found.

Pseudo code for Boyer–Moore Pattern Matching algorithm

Boolean BoyerMoore( T: text, P: pattern)
n: length of T,      i: index of T
m: length of P,      j: index of P
bctable[ch] is an array, for ch = 0 to 127 (ASCIl values)

1. Initialize all elements of array bctable to m.
2. Set bctable[Pj] = m-j-1, for j= 0 to m-1.
3. Initialize i = m-1
4. Repeat steps 5 to 8, while(i < n) 
5. j := m-1
6. Repeat steps (a) and (b), while (j ≥ 0 and Pj = Ti)
    (a) decrement i
    (b) decrement j
7. if (j = -1) return true     //pattern matching successful
8. i := i+ max(bctable[Ti], m-j)
9. return false              //at the end, if pattern matching fails, return false

Brute-force v/s Boyer-Moore pattern matching algorithms

The Brute-force algorithm compares every character in the text T to locate a pattern P as a substring. In contrast, the Boyer-Moore (BM) pattern matching algorithm can avoid comparisons between P and a significant portion of the characters in T. While the brute-force algorithm works with any alphabet, the BM algorithm assumes a fixed, finite alphabet. The BM algorithm performs fastest when the alphabet is moderately sized and the pattern is long. Thus, BM is ideal for searching words in documents. This simplified BM algorithm matches P to T by comparing right-to-left instead of left-to-right. Upon a mismatch, it shifts P right and restarts matching from P's end. This right-shift skips over T characters not involved in the comparisons. In this way, BM gains speed by skipping comparisons.